A Class of Models with the Potential to Represent Fundamental Physics
  1. Introduction
  2. Basic Form of Models
  3. Typical Behaviors
  4. Limiting Behavior and Emergent Geometry
  5. The Updating Process for String Substitution Systems
  6. The Updating Process in Our Models
  7. Equivalence and Computation in Our Models
  8. Potential Relation to Physics
  9. Additional Material
  10. References
  11. Index
Download PDf download pdf
ARXIV ARXIV
peer-review peer review
technical introduction Limiting Behavior and Emergent Geometry

4.8 Homogeneity and Local Graph Neighborhoods

In studying Vr we are looking at the total size of the neighborhood up to distance r around a point in a graph. But what about the actual local structure of the neighborhood?

In general, it can be different for every point on the graph. Thus, for example, in

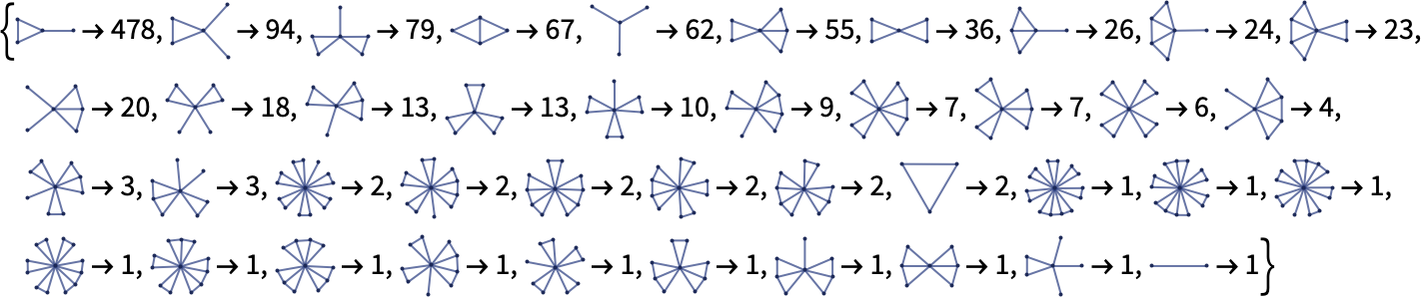
obtained from 10 steps of the rule {{x,y},{x,z}}{{x,z},{x,w},{y,w},{z,w}} the collection of distinct range-1 neighborhoods (with their counts) is:

The corresponding result after 12 steps is:

And it seems that for this rule the distribution of different forms for a given range of neighborhood generally stabilizes as the number of steps increases. (It may be possible to characterize it as limiting to an invariant measure in the space of possible hypergraphs, perhaps with some related entropy (cf. [1:p958][31]).)

One sees the same kind of stabilization for most rules, though, for example, in a case like

from the rule {{x,y}}{{x,y},{y,z},{z,x}} one always gets some neighborhoods with new forms at each step:

In general, the presence of many identical neighborhoods reflects a certain kind of approximate symmetry or isometry of the emergent geometry of the system.

In a torus graph, for example, the symmetry is exact, and all local neighborhoods of a given range are the same:

The same is true for a 3D torus graph:

For a sphere graph not every point has the exact same local neighborhood, but there are a limited number of neighborhoods of a given range:

And from the dual graph it becomes clear that these are associated with hexagonal and pentagonal “faces”:

For a (spherical) Sierpiński graph, there are also a limited number of neighborhoods of a given range:

Whenever every local neighborhood is essentially identical, Vr(X) will have the same form for every point X in a graph or hypergraph. But in general Vr(X) (and the log differences Δr(X)) will depend on X. The picture below shows the relative values of Δr(X) at each point in the structure we showed above:

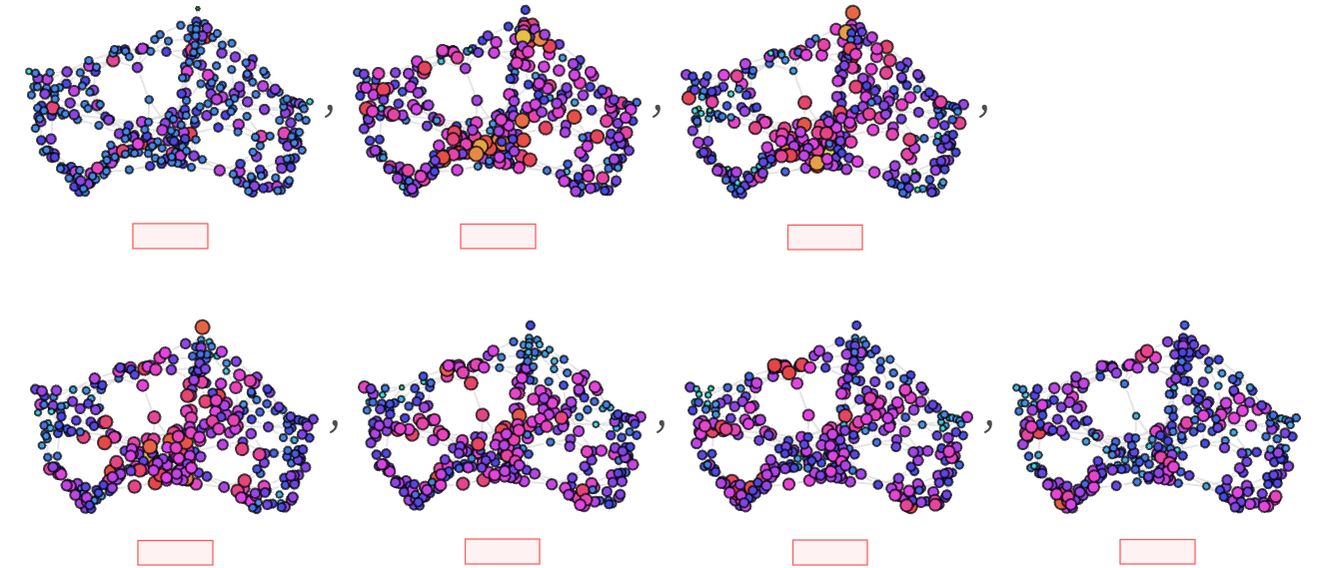
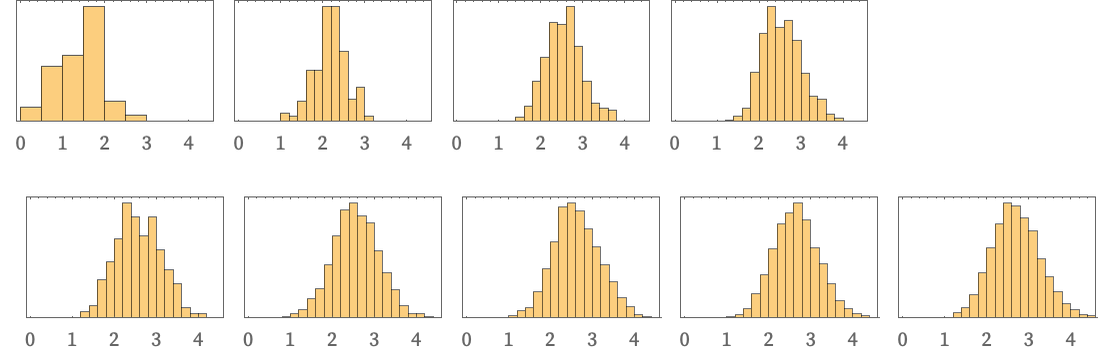
We can also compute the distribution of values for Δr(X) across the structure, as a function of r:

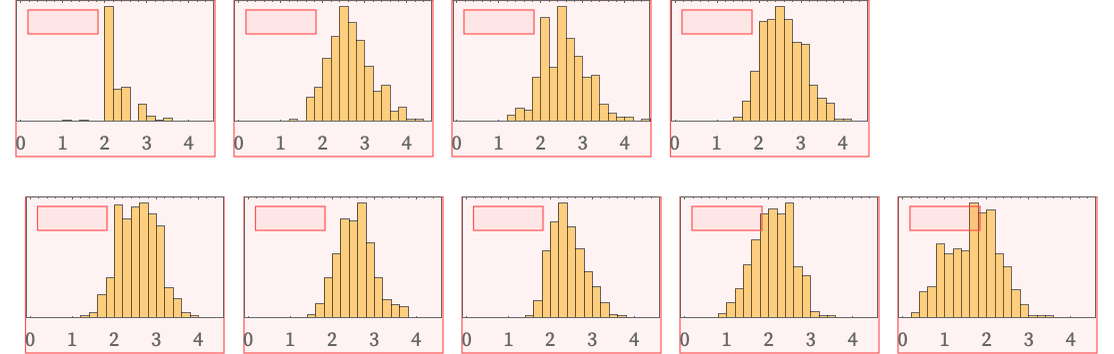
Both these pictures indicate a certain statistical uniformity in Vr(X). This is also seen if we look at the evolution of the distribution of Δr(X), here shown for the specific value r = 6, for steps 8 through 16:

  • Download Notebook
  • Open in Wolfram Cloud
  • Discuss This Page