We saw above a rule which generates a sequence of hypergraphs like this:

We can think of this after an infinite number of steps as giving an infinitely fine mesh—or in effect a structure which limits to a two-dimensional manifold. In standard mathematics, the defining feature of a manifold is that it is locally like Euclidean space (in some number of dimensions d) [45]. By using Euclidean space as a model many things can be defined and computed about manifolds (e.g. [26]).
Some of our models here yield emergent geometry whose limit is an ordinary manifold. But the question arises of what mathematical structures might be appropriate for describing the limiting behavior of other cases. Is there perhaps some other kind of model space whose properties can be transferred?
It is tempting to try to start from Euclidean space (or n), and define some subset such as a Cantor set. But it seems more likely to be fruitful to start from convenient discrete structures, and see how their limits might correspond to what we have. One important feature of Euclidean space is its uniformity: every point is in a sense like every other, even if different points can be labeled by different coordinates.
So this suggests that by analogy we could consider graphs (and hypergraphs) whose vertices all have the same graph neighborhood (vertex transitive graphs). Several obvious infinite examples are the limits of:

Any uniform tessellation or regular tree provides an example. One might think that another example would be graphs formed by uniform application of a vertex substitution rule—such as “spherical Sierpiński graphs” starting from a tetrahedron, dodecahedron or buckyball graph:
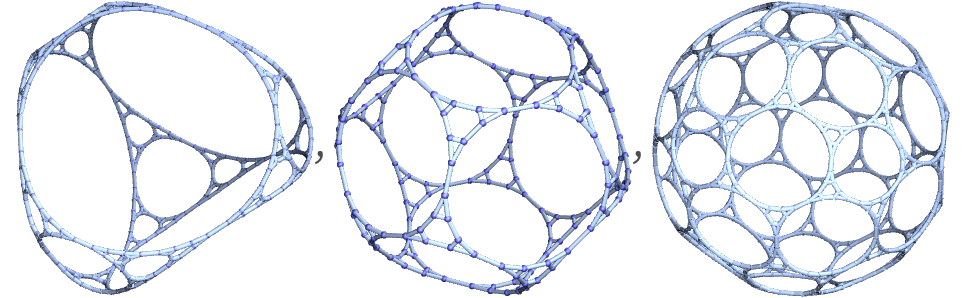
But (as mentioned in 4.8) in these graphs not every vertex has exactly the same neighborhood, at least if one goes beyond geodesic distance 2. The number of distinct neighborhoods does, however, grow fairly slowly, suggesting that it may be possible to consider such graphs “quasi vertex transitive” (in rough analogy to quasiconformal).
But one important class of graphs that are precisely vertex transitive are Cayley graphs of groups—and indeed the infinite tessellation and tree graphs above are all examples of these. (Note that not all vertex-transitive graphs are Cayley graphs; the Petersen graph is an example [46]. It is also known that there are infinite vertex-transitive graphs that are not Cayley graphs [47], and are not even “close” to any such graphs [48].)
In a Cayley graph for a group, each node represents an element of the group, and each edge is labeled with a generator of the group. (Different presentations of the group—with different choices of generators and relations—can have slightly different Cayley graphs, but their infinite limits can be considered the same.) Each point in the Cayley graph can then be labeled (typically not uniquely) by a word in the group, specified as a product of generators of the group.
One can imagine progressively building up a Cayley graph by looking at longer and longer words. In the case of a free group with two generators A and B, this yields:
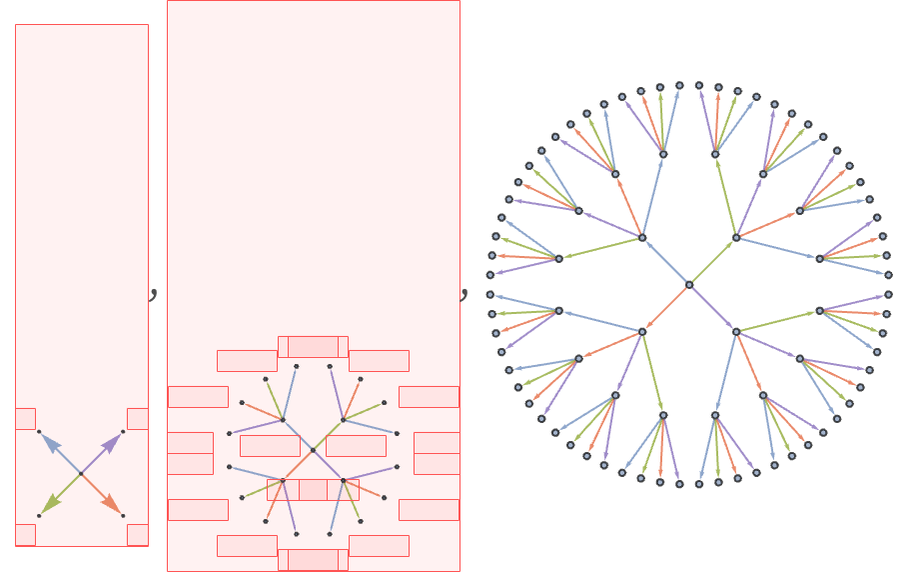
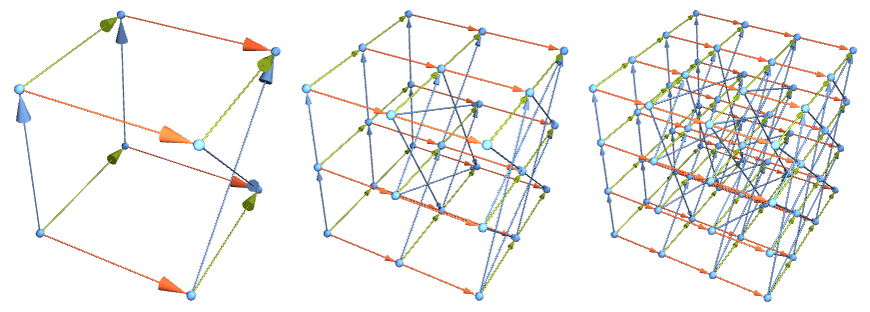
If one adds the relation AB = BA, defining an Abelian group, the Cayley graph is instead a grid, with “coordinates” given by the numbers of As and Bs (or their inverses):
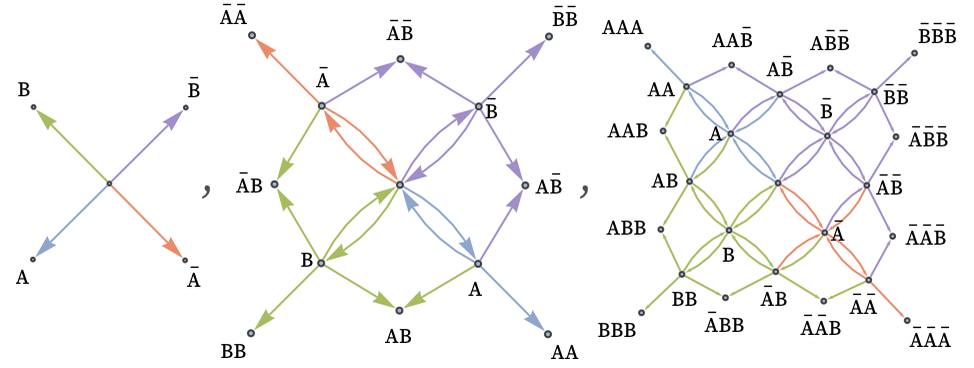
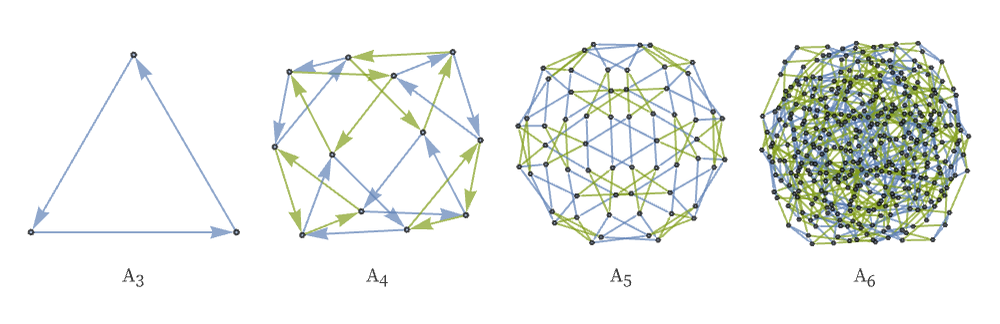
Here are the Cayley graphs for the first few symmetric and alternating (finite) groups:
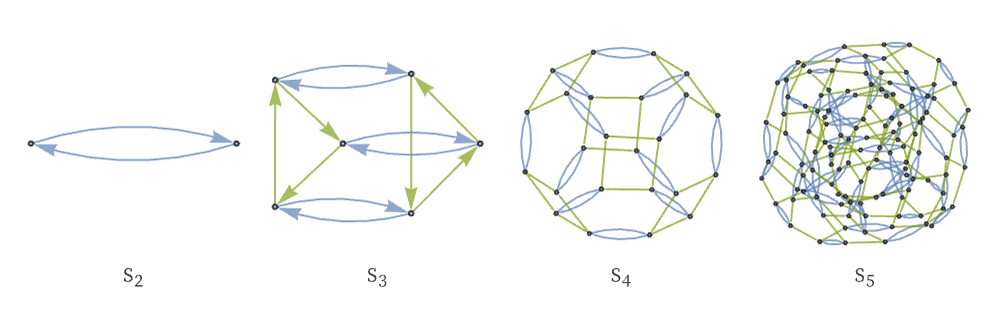
For a given infinite Cayley graph, one can compute a limiting Vr just as we have for hypergraphs. If one picks a finite number of generators and relations at random, one will usually get a Cayley graph that has a basically tree-like structure, with a Vr that grows exponentially. For nilpotent groups, however, Vr always has polynomial growth—an example being the Heisenberg group H3 whose Cayley graph is the limit of [49]:
There are also groups known that yield growth intermediate between polynomial and exponential [50]. There do not, however, appear to be groups that yield fractional-power growth, corresponding to finite but fractional dimension.
It is possible that one could view the evolution of one of our models as being directly analogous to the growth of the Cayley graph for a group—or at least somehow approximated by it. As we discussed above, the hypergraphs generated by most of our systems are not, however, uniform, in the sense that the structures of the neighborhoods around different points in the hypergraph can be different. But this does not mean that a Cayley graph could not provide a good (at least approximate) local model for a part of the hypergraph. And if this connection could be made, there might be useful results from modern geometric group theory that could be applied, for example in classifying different kinds of limiting behaviors of our systems.
On a sufficiently small scale, any manifold is defined to be like Euclidean space. But if one goes to a slightly larger scale, one needs to represent deviations from Euclidean space. And a convenient way to do this is again to consider model spaces. The most obvious is a sphere (or in general a hyperellipsoid)—and this is what gives the notion of curvature. Quite what the appropriate analog even of this is in fractional dimensional space is not clear, but it would potentially be useful in studying our systems. And when there is a possibility for change in dimension as well as change in curvature, the situation is even less clear.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review