A Class of Models with the Potential to Represent Fundamental Physics
  1. Introduction
  2. Basic Form of Models
  3. Typical Behaviors
  4. Limiting Behavior and Emergent Geometry
  5. The Updating Process for String Substitution Systems
  6. The Updating Process in Our Models
  7. Equivalence and Computation in Our Models
  8. Potential Relation to Physics
  9. Additional Material
  10. References
  11. Index
Download PDf download pdf
ARXIV ARXIV
peer-review peer review
technical introduction Limiting Behavior and Emergent Geometry

4.14 The Effect of Perturbations

Imagine that at some step in the evolution of a rule one reverses a single relation. What effect will it have? Here is an example for the rule {{x,y},{x,z}}{{x,z},{x,w},{y,w},{z,w}}. The first row is the original evolution; the second is the evolution after reversing the relation:

We can illustrate the effect by coloring edges in the first row of graphs that are different in the second one (taking account of graph isomorphism) [41]:

Visualizing the second and third graphs in 3D makes it more obvious that the changed edges are mostly connected:

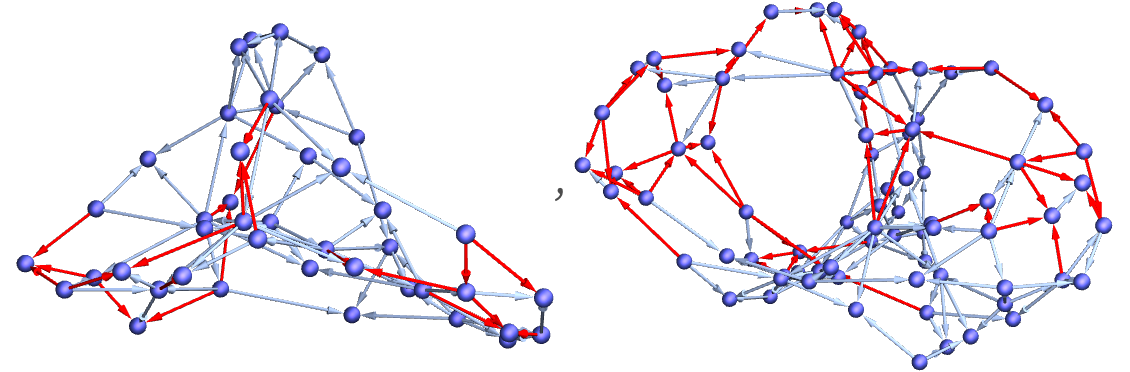
It takes only a few steps before the effect of the change has spread to essentially all parts of the system. (In this particular case, with the updating order used, about 20% of edges are still unaffected after 5 steps, with the fraction slowly decreasing, even as the number of new edges increases.)

In rules with fairly simple behavior, it is common for changes to remain localized:

However, when complex behavior occurs, changes tend to spread. This is analogous to what is seen, for example, in the much simpler case of class 2 versus class 3 cellular automata [31][1:6.3]:

Cellular automata are also known [31] to exhibit the important phenomenon of class 4 behavior—in which there is a discrete set of localized “particle-like” structures through which changes typically propagate:

In cellular automata, there is a fixed lattice on which local rules operate, making it straightforward [1:6.3] to identify the region that can in principle be affected by a change in initial conditions. In the models here, however, everything is dynamic, and so even the question of what parts can in principle be affected by a change in initial conditions is nontrivial.

As we will discuss at length later, however, it is always possible to trace which updating events in a particular evolution depend on which others, and which relations are associated with these. The result will always be a superset of the actual effect of a change in the initial condition:

We discussed above the quantity Vr(X) obtained by “statically” looking at the number of nodes in a hypergraph reached by going graph distance r—in effect computing the volume of a ball of radius r in the hypergraph. By looking at the dependence of updating events in t successive steps of evolution, we can define another quantity Ct(X) which in effect measures the volume of a cone of dependencies in the evolution of the system.

Vr(X) is in a sense a quantity that is “applied” to the system from outside; Ct(X) is in a sense intrinsic. But as we will discuss later, Vr(X) is in some sense an approximation to Ct(X)—and particularly when we can reasonably consider the evolution of a model to have reached some kind of “equilibrium”, Vr(X) will provide a useful characterization of the “state” of a model.

  • Download Notebook
  • Open in Wolfram Cloud
  • Discuss This Page