4.5 The Notion of Dimension

In traditional geometry, a basic feature of any continuous space is its dimension. And we have seen that at least in certain cases we can characterize the limiting behavior of our models in terms of the emergence of recognizable geometry—with definite dimension. So this suggests that perhaps we might be able to use a notion of dimension to characterize the limiting behavior of our models even when we do not readily recognize traditional geometrical structure in them.

For standard continuous spaces it is straightforward to define dimension, normally in terms of the number of coordinates needed to specify a position. If we make a discrete approximation to a continuous space, say with a progressively finer grid, we can still identify dimension in terms of the number of coordinates on the grid. But now imagine we only have a connectivity graph for a grid. Can we deduce what dimension it corresponds to?

We might choose to draw the grids so they lay out according to coordinates, here in 1-, 2- and 3-dimensional Euclidean space:

But these are all the same graph, with the same connectivity information:

So just from intrinsic information about a graph—or, more accurately, from information about a sequence of larger and larger graphs—can we deduce what dimension of space it might correspond to?

The procedure we will follow is straightforward (cf. [1:p479][22]). For any point X in the graph define V_r(X) to be the number of points in the graph that can be reached by going at most graph distance r. This can be thought of as the volume of a ball of radius r in the graph centered at X.

For a square grid, the region that defines V_r(X) for successive r starting at a point in the center is:

For an infinite grid we then have:

For a 1D grid the corresponding result is:

And for a 3D grid it is:

In general, for a d-dimensional cubic grid (cf. [1:p1031]) the result is a terminating hypergeometric series (and the coefficient of z^d in the expansion of (z + 1)^r/(z – 1)^r+1):

But the important feature for us is that the leading term—which is computable purely from connectivity information about the graph—is proportional to r^d.

What will happen for a graph that is less regular than a grid? Here is a graph made by random triangulation of a 2D region:

And once again, the number of points reached at graph distance r grows like r²:

In ordinary d-dimensional continuous Euclidean space, the volume of a ball is exactly

And we should expect that if in some sense our graphs limit to d-dimensional space, then in correspondence with this, V_r should always show r^d growth.

There are, however, many subtle issues. The first—immediately evident in practice—is that if our graph is finite (like the grids above) then there are edge effects that prevent r^d growth in V_r when the radius of the ball becomes comparable to the radius of the graph. The pictures below show what happens for a grid with side length 11, compared to an infinite grid, and the r^d term on its own:

One might imagine that edge effects would be avoided if one had a toroidal grid graph such as:

But actually the results for V_r(X) for any point on a toroidal graph are exactly the same as those for the center point in an ordinary grid; it is just that now finite-size effects come from paths in the graph that wrap around the torus.

Still, so long as r is small compared to the radius of the graph—but large enough that we can see overall r^d growth—we can potentially deduce an effective dimension from measurements of V_r.

In practice, a convenient way to assess the form of V_r, and to make estimates of dimension, is to compute log differences as a function of r:

Here are results for the center points of grid graphs (or for any point in the analogous toroidal graphs):

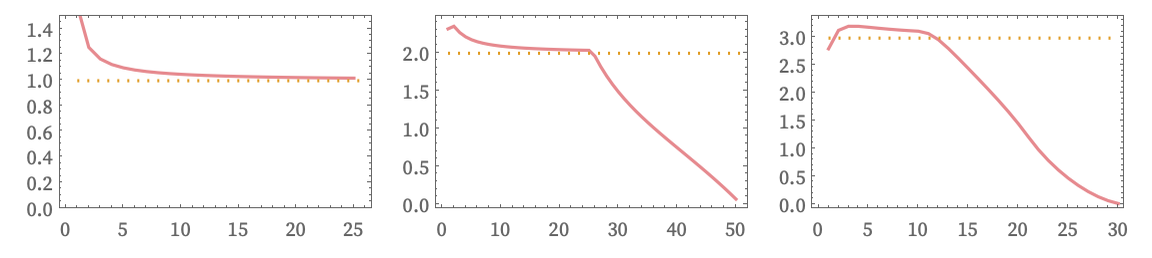
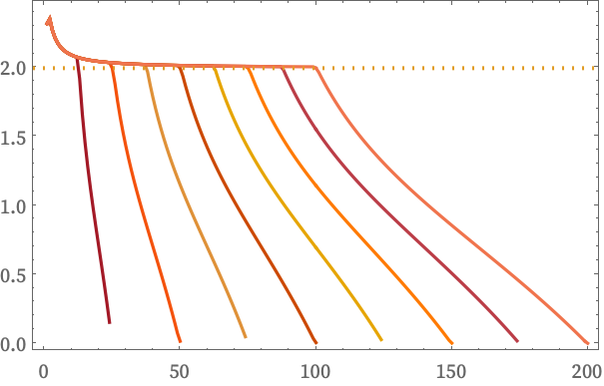
The results are far from perfect. For small r one is sensitive to the detailed structure of the grid, and for large r to the finite overall size of the graph. But, for example, for a 2D grid graph, as the size of the graph is progressively increased, we see that there is an expanding region of values of r at which our estimate of dimension is accurate:

A notable feature of measuring dimension from the growth rate of V_r(X) is that the measurement is in some sense local: it starts from a particular position X. Of course, in looking at successively larger balls, V_r(X) will be sensitive to parts of the graph progressively further away from X. But still, the results can depend on the choice of X. And unless the graph is homogeneous (like our toroidal grids above), one will often want to average over at least a range of possible positions X. Here is an example of doing such averaging for a collection of starting points in the center of the random 2D graph above. The error bars indicate 1σ ranges in the distribution of values obtained from different points X.

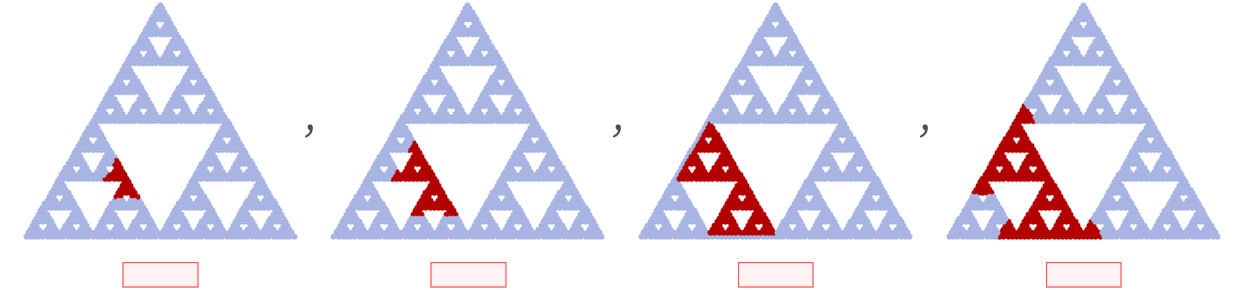
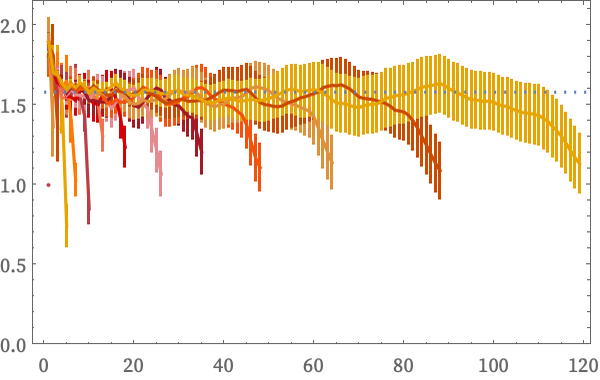
So far we have looked at graphs that approximate standard integer-dimensional spaces. But what about fractal spaces [23]? Let us consider a Sierpiński graph, and look at the growth of a ball in the graph:

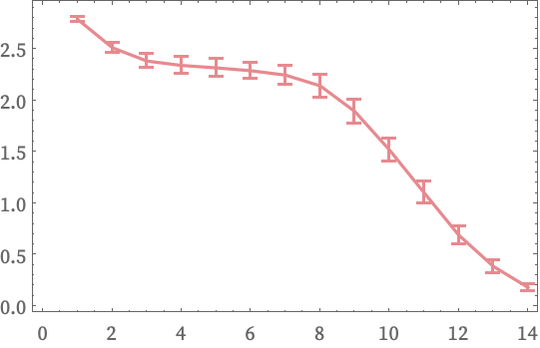
Estimating dimension from V_r(X) averaged over all points we get (for graphs made from 6 and 7 recursive subdivisions):

The dotted line indicates the standard Hausdorff dimension log₂(3)≈1.58 for a Sierpiński triangle [23]. And what the pictures suggest is that the growth rate of V_r approximates this value. But to get the exact value we see that in addition to everything else, we will need average estimates of dimension over different values of r.

In the end, therefore, we have quite a collection of limits to take. First, we need the overall size of our graph to be large. Second, we need the range of values of r for measuring V_r to be small compared to the size of the graph. Third, we need these values to be large relative to individual nodes in the graph, and to be large enough that we can readily measure the leading order growth of V_r—and that this will be of the form r^d. In addition, if the graph is not homogeneous we need to be averaging over a region X that is large compared to the size of inhomogeneities in the graph, but small compared to the values of r we will use in estimating the growth of V_r. And finally, as we have just seen, we may need to average over different ranges of r in estimating overall dimension.

If we have something like a grid graph, all of this will work out fine. But there are certainly cases where we can immediately tell that it will not work. Consider, for example, first the case of a complete graph, and second of a tree:

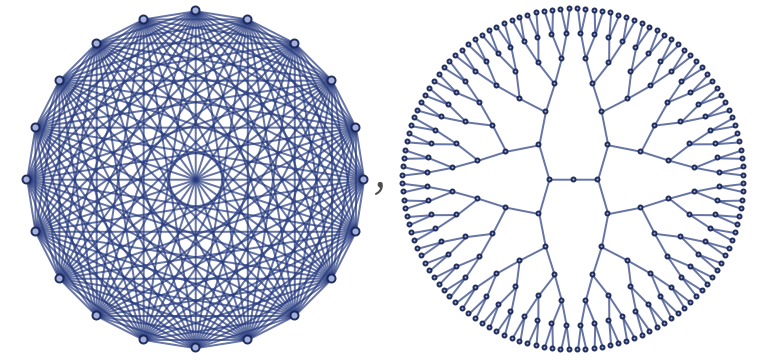
For a complete graph there is no way to have a range of r values “smaller than the radius of graph” from which to estimate a growth rate for V_r. For a tree, V_r grows exponentially rather than as a power of r, so our estimate of dimension Δ(r) will just continually increase with r:

But notwithstanding these issues, we can try applying our approach to the objects generated by our models. As constructed, these objects correspond to directed graphs or hypergraphs. But for our current purposes, we will ignore directedness in determining distance, effectively taking all elements in a particular k-ary relation—regardless of their ordering—to be at unit distance from each other.

As a first example, consider the 2₃  3₃ rule we discussed above that “knits” a simple grid:

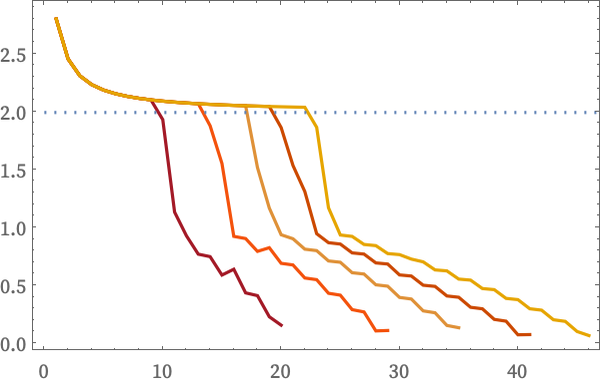
As we run the rule, the structure it produces gets larger, so it becomes easier to estimate the growth rate of V_r. The picture below shows Δ(r) (starting at the center point) computed after successively more steps. And we see that, as expected, the dimension estimate appears to converge to value 2:

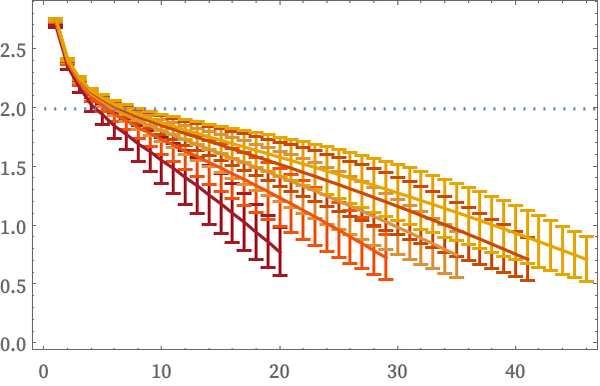
It is worth mentioning that if we did not compute V_r(X) by starting at the center point, but instead averaged over all points, we would get a less useful result, dominated by edge effects:

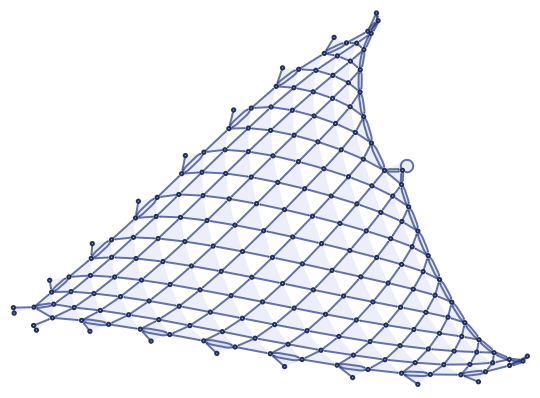
As a second example, consider the 2₃  3₃ rule that slowly generates a somewhat complex kind of surface:

As we run this longer, we see what appears to be increasingly close approximation to dimension 2, reflecting the fact that even though we can best draw this object embedded in 3D space, its intrinsic surface is two-dimensional (though, as we will discuss later, it also shows the effects of curvature):

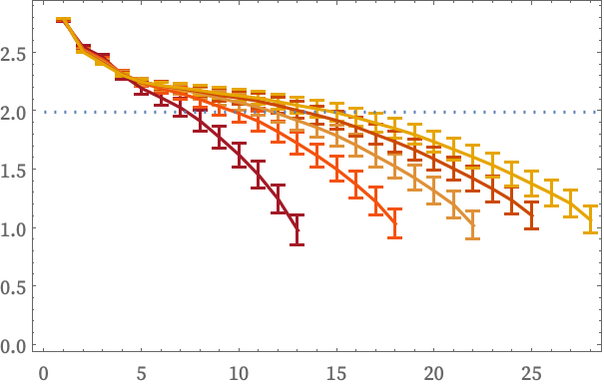
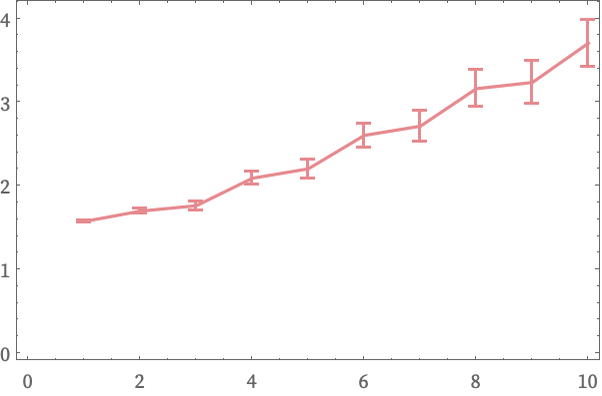
The successive dimension estimates shown above are spaced by 500 steps in the evolution of the rule. As another example, consider the 2₃1₂  4₃4₂ rule, in which geometry emerges rapidly through a process of subdivision:

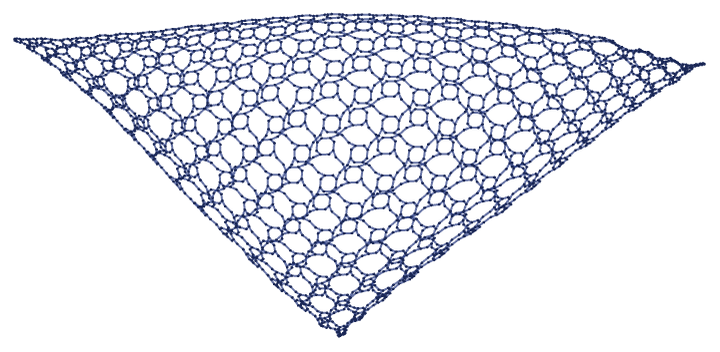
These are dimension estimates for all of the first 10 steps in the evolution of this rule:

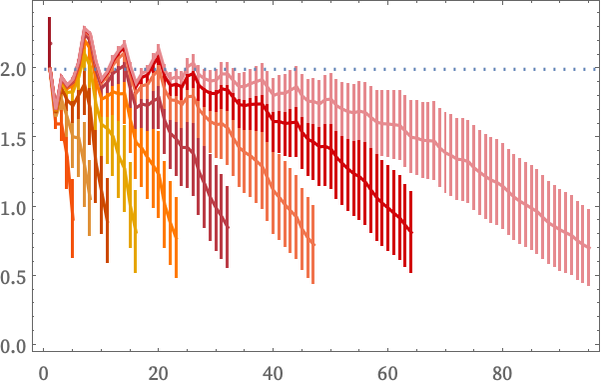
We can also validate our approach by looking at rules that generate obviously nested structures. An example is the 2₂  4₂ rule that produces:

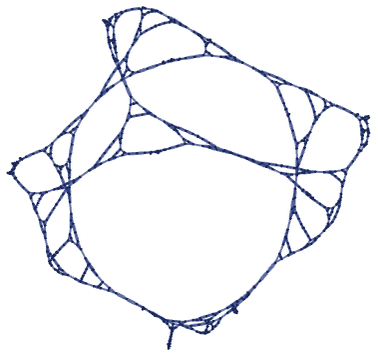
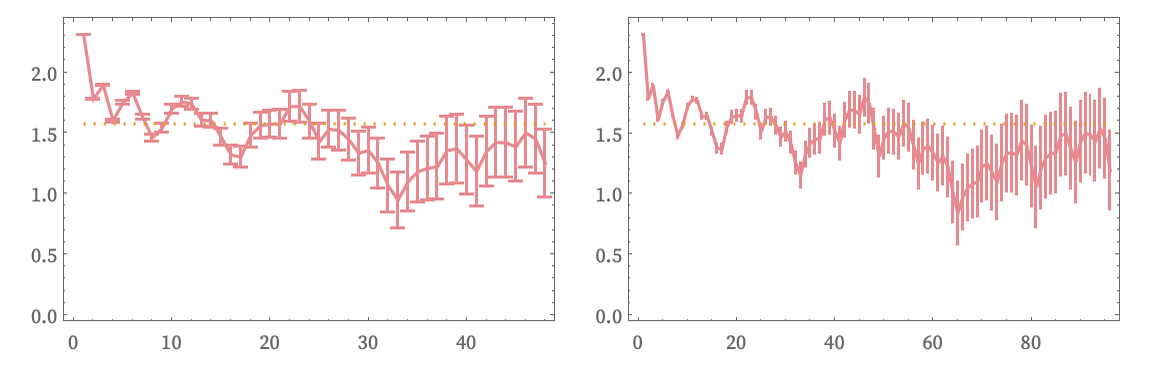
The results for each of the first 15 steps show good correspondence to dimension log₂(3)≈1.58: