8.9 Elementary Particles

Elementary particles are entities that—at least for some period—preserve their identity through space and time. In the context of our models, one can imagine that particles would correspond to structures in the hypergraph that are locally stable under the application of rules.

As an idealized example, consider rules that operate on an ordinary graph, and have the property of preserving planarity. Such rules can never remove non-planarity from a graph. But it is a basic result of graph theory [37][118] that any non-planarity can always be attributed to one of the two specific subgraphs:

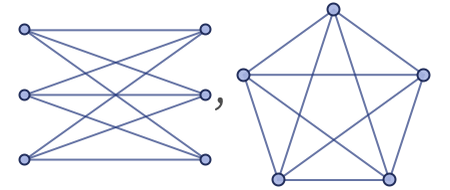
If one inserts such subgraphs into an otherwise planar graph, they behave very much as “particle-like” structures. They can move around, but unless they meet and annihilate, they are preserved:

There are presumably analogs of this in hypergraph-rewriting rules of the kind that appear in our models. Given a particular set of rules, the expectation would be that a certain set of local sub-hypergraphs would be preserved by the rules. Existing results in graph theory do not go very far in elucidating the details.

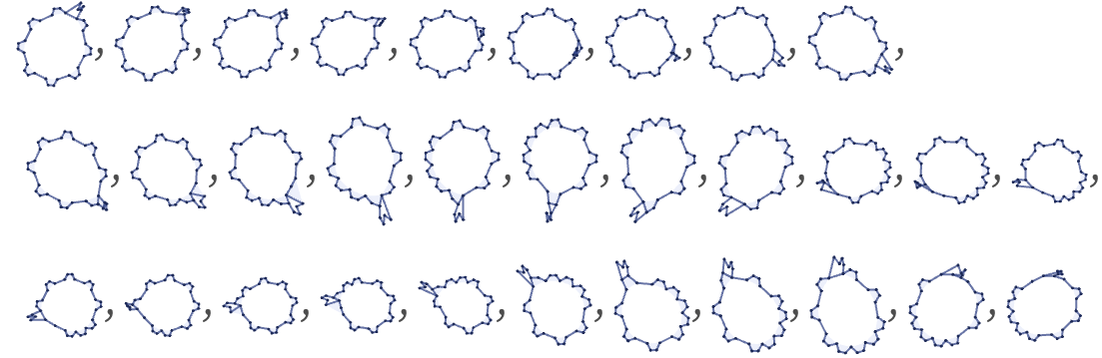
However, there are analogs in other systems that provide some insight. Cellular automata provide a particularly good example. Consider the rule 110 cellular automaton [1:p32]. Starting from a random initial condition, the picture below shows how the system evolves to a collection of localized structures:

The form of these structures is hard to determine directly from the rule. (They are a little like hard-to-predict solutions to a Diophantine equation.) But by explicit computation one can determine for example that rule 110 supports the following types of localized structures [1:p292][119]

as well as the growing structure:

There is a complex web of possible interactions between localized structures, that can at least in some cases be interpreted in terms of conservation laws:

As in cellular automata, it is likely that not every one of our models will yield localized structures, although there is reason to think that some form of conserved structure will be more common in hypergraph rewriting than in cellular automata. But as in cellular automata, one can expect that with a given underlying rule, there will be a discrete set of possible localized structures, with hard-to-predict sizes and properties.

The particular set of localized structures will probably be quite specific to particular rules. But as we will discuss in the next subsection, there will often be symmetries that cause collections of similar structures to exist—or in fact force certain structures to exist.

In the previous subsection, we discussed the interpretation of energy and momentum in terms of additional edges in a causal graph. For particles, the expectation would be that there is a certain “core” structure that defines the core properties of a particle (like spin, charge, etc.), but that this structure is spread across a region of the hypergraph that maintains the “activity” associated with energy and momentum.

It is worth noting that even in an example like non-planarity, it is perfectly possible for topological-like features to effectively be spread out across many nodes, while still maintaining their discrete character.

In the previous subsection, we discussed the potential origin of rest mass in terms of “reuse” of nodes in the hypergraph. Once again, this seems to fit in well with our notion of the nature of particles—and to make it perfectly possible to imagine both “massive” and “massless” particles, associated with different kinds of structures in the evolving hypergraph.

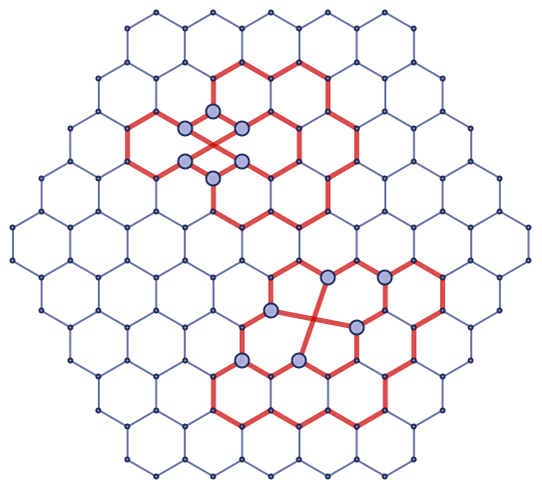
In a system like the rule 110 cellular automaton, there is a clear “background structure” on which it is possible to identify localized structures. In some very simple cases, similar things happen in our models. For example, consider the rule:

The evolution of this rule yields behavior like

in which there is a circular “background”, with a localized “particle-like” deformation. The causal graph (here generated for a larger case) also shows evidence of a particle-like structure on a simple grid-like background:

But in most of our models the “background” tends to be much more complicated, and so such direct methods for identifying particles cannot be used. But as an alternative, one can consider exploring the effect of perturbations, as in 4.14. In effect, one starts the system with a perturbation, then sees whether the perturbation somehow decomposes into quantized elements that one can identify as “particles”. (The process is quite analogous to producing particles in a high-energy collision.)

Such quantized effects are at best rare in class 3 cellular automata, but they are a defining feature of class 4 cellular automata, and there is reason to believe that they will be at least fairly common in our models.

The defining feature of a localized “particle-like” structure is that it is capable of long-range propagation in the system. But the presence of even short-lived instances of particle-like structures will also potentially be identifiable—though with a certain margin of error—from detailed properties of the hypergraph in small regions. And in the “background” evolution of our models, one can expect that short-lived instances of particle-like structures will continually be being created and destroyed.

The process that in a sense “creates the structure of space” in our models can thus also be thought of as producing a “vacuum” full of particle-like activity. And particularly when this is combined with the phenomenon (to be discussed in a later subsection) that pairs of particle-like structures can be produced and subsequently merged in the multiway system, there is some definite similarity with the ubiquitous virtual particles that appear in traditional treatments of quantum field theory.