8.22 Multiway Systems in the Space of All Possible Rules

We have discussed the possibility that our physical universe might be described as following a model of the type we have introduced here, with a particular rule. And to find such a rule would be a great achievement, and might perhaps be considered a final answer to the core question of fundamental physics.

But if such a rule is found, one might then go on and ask why—out of the infinite number of possibilities—it is this particular rule, or, for example, a simple rule at all. And here the paradigm we have developed makes a potential additional suggestion: perhaps there is not just one rule being used after all, but instead in a sense all possible rules are simultaneously used.

In the multiway systems we have discussed so far, there is a single underlying rule, but separate branches for all possible sequences of updating events. But one can imagine a rule-space multiway system, that includes branches not only for every sequence of updating events, but also for every possible rule used to do the updating. Somewhat like with updating events, there will be many states reached to which many of the possible rules cannot apply. (For example, a rule that involves only ternary edges cannot apply to a state with only binary edges.) And like with updating events, branches with different sequences of rules applied may reach equivalent states, and thus merge.

Operationally, it is not so difficult to see how to set up a rule-space multiway system. All it really involves is listing not just one or a few possible rules that can be used for each updating event, but in a sense listing all possible rules. In principle there are an infinite number of such rules, but any rule that involves rewriting a hypergraph that is larger than the hypergraph that represents the whole universe can never apply, so at least at any given point in the evolution of the system, the number of rules to consider is finite. But like with the many other kinds of limits we have discussed, we can still imagine taking the limit of all infinitely many possible rules.

As a toy example of a rule-space multiway system, consider all inequivalent 2  2 rules on strings of As and Bs:

We can immediately construct the rule-space multiway graph for these rules (here starting from all possible length-4 sequences of As and Bs):

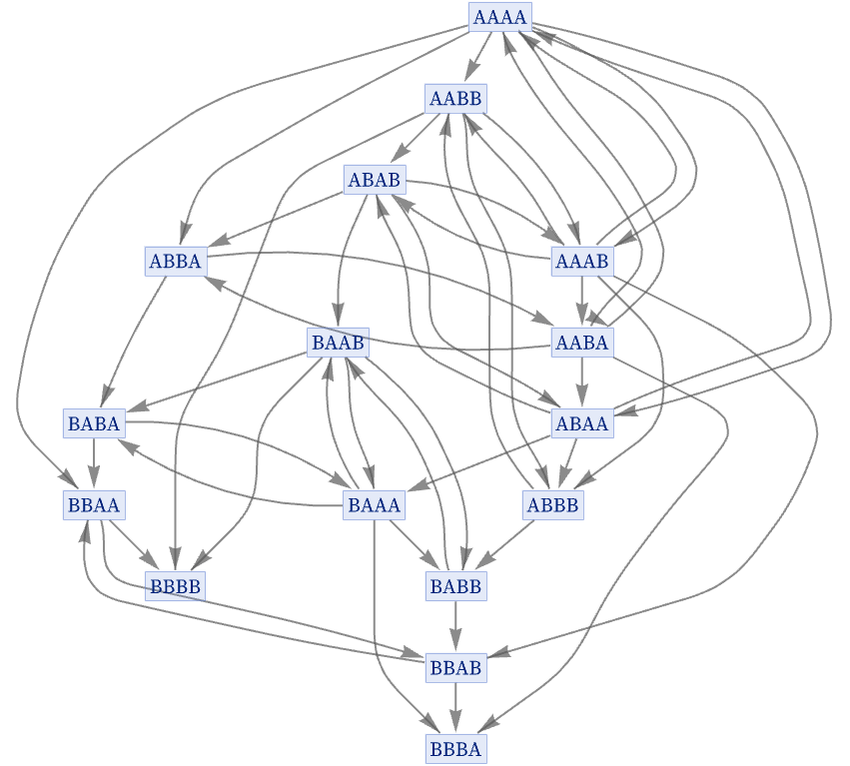
Different branches of the rule-space multiway system use different rules:

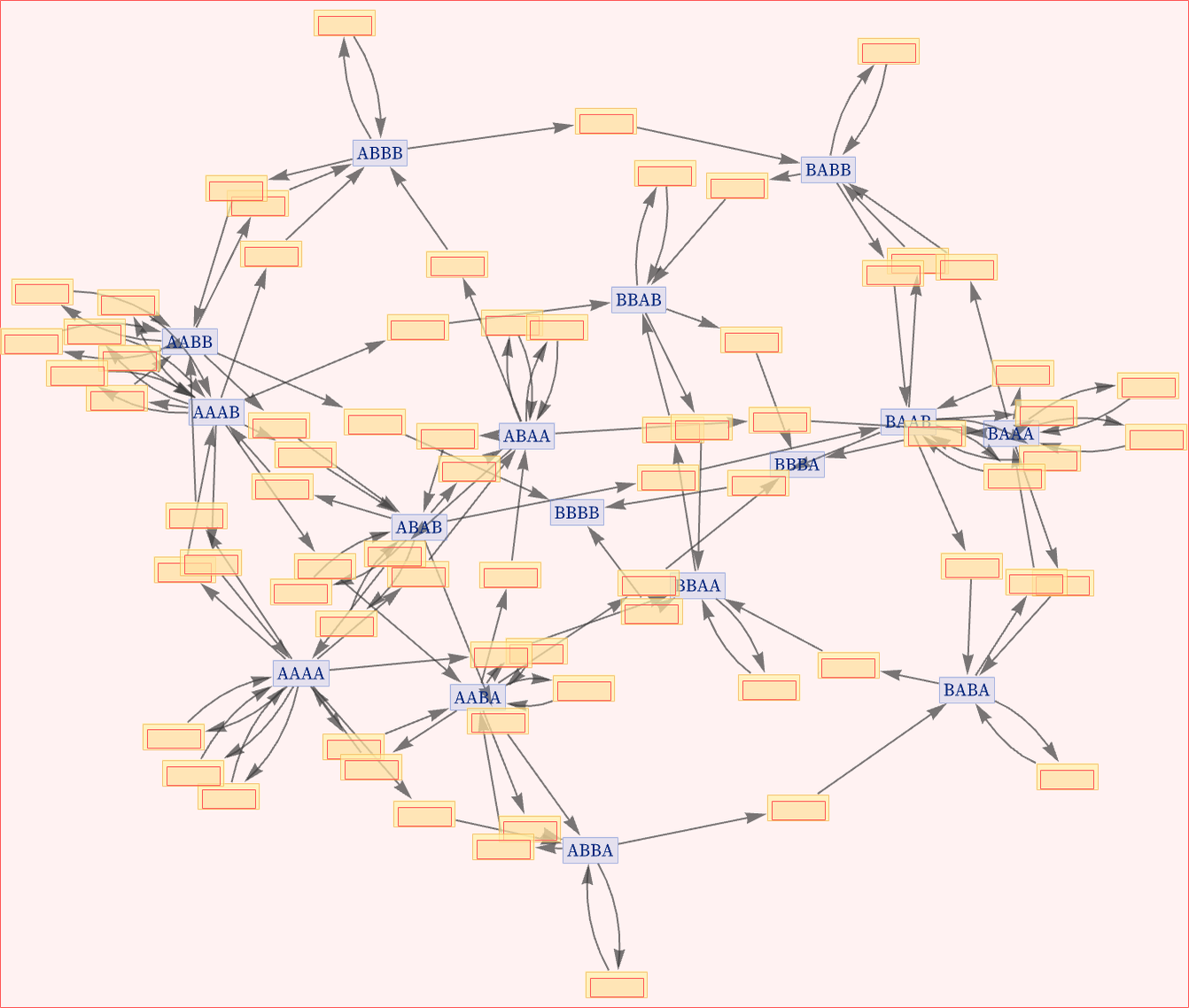
One can include causal connections:

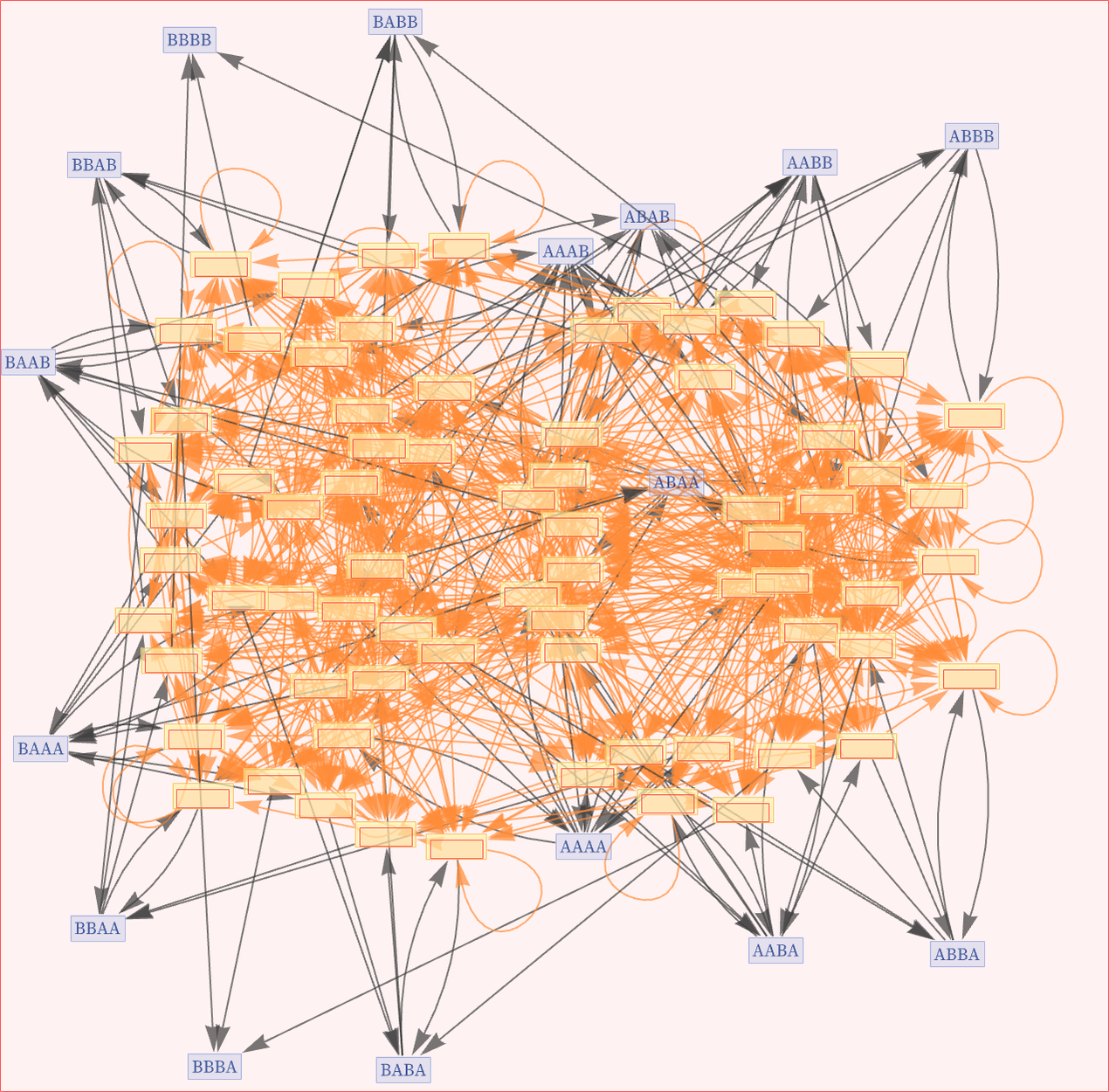
But even removing multiedges, the full rule-space multiway causal graph is complicated:

The “branchial graph” of the rule-space multiway system, though, is fairly simple, at least after one step (though it is now really more of a “rule-space graph”):

At least in this toy example, we already see something important: the rule-space multiway system is causal invariant: given branching even associated with using different rules, there is always corresponding merging—so the graph of causal relationships between updating events, even with different rules, is always the same.

Scaling up to unbounded evolutions and unbounded collections of rules involves many issues. But it seems likely that causal invariance will survive. And ultimately one may anticipate that across all possible rules it will emerge as a consequence of the Principle of Computational Equivalence [1:12]. Because this principle implies that in the space of all possible rules, all but those with simple behavior are equivalent in their computational capabilities. And that means that across all the different possible sequences of rules that can be applied in the rule-space multiway system there is fundamental equivalence—with the result that one can expect causal invariance.

But now consider the role of the observer, who is inevitably embedded in the system, as part of the same rule-space multiway graph as everything else. Just as we did for ordinary multiway graphs above, we can imagine foliating the rule-space multiway graph, with the role of space or branchial space now being taken by rule space. And one can think of exploring rule space as effectively corresponding to sampling different possible descriptions of how the universe works, based on different underlying rules.

But if each event in the rule-space multiway graph is just a single update, based on a particular (finite) rule, there is immediately a consequence. Just like with light cones in ordinary space, or entanglement cones in branchial space, there will be a new kind of cone that defines a limit on how fast it is possible to “travel” in rule space.

For an observer, traveling in rule space involves ascribing different rules to the universe, or in effect changing one’s “reference frame” for interpreting how the universe operates. (An “inertial frame” in rule space would probably correspond to continuing to use a particular rule.) But from the Principle of Computational Equivalence [1:12] (and specifically from the idea of computation universality (e.g. [1:11])) it is always possible to set up a computation that will translate between interpretations. But in a sense the further one goes in rule space, the more difficult the translation may become—and the more computation it will require.

But now remember that the observer is also embedded in the same system, so the fundamental rate at which it can do computation is defined by the structure of the system. And this is where what one might call the “translation cone” comes from: to go a certain “distance” in rule space, the observer must do a certain irreducible amount of computational work, which takes a certain amount of time.

The maximum rate of translation is effectively a ratio of “rule distance” to “translation effort” (measured in units of computational time). In a sense it probes something that has been difficult to quantify: just how “far apart” are different description languages, that involve different computational primitives? One can get some ideas by thinking about program size [144][145][146], or running time, but in the end new measures that take account of things, like the construction of sequences of abstractions, seem to be needed [147].

For our current discussion, however, the main point is the existence of a kind of “rule-space relativity”. Depending on how an observer chooses to describe our universe, they may consider a different rule—or rather a different branch in the rule-space multiway system—to account for what they see. But if they change their “description frame”, causal invariance (based on the Principle of Computational Equivalence) implies that they will still find a rule (or a branch in the rule-space multiway system) that accounts for what they see, but it will be a different one.

In the previous section, we discussed equivalences between our models and other formulations. The fact that we base our models on hypergraph rewriting (or any of its many equivalent descriptions) is in a sense like a choice of coordinate system in rule space—and there are presumably infinitely many others we could use.

But the fact that there are many different possible parametrizations does not mean that there are not definite things that can be said. It is just that there is potentially a higher level of abstraction that can be reached. And indeed, in our models, not only have we abstracted away notions of space, time, matter and measurement; now in the rule-space multiway system we are in a sense also abstracting away the very notion of abstraction itself (see also [2]).