There are 79,359,764 inequivalent left-connected 23 33 rules. The fraction of these rules showing continued growth is considerably smaller than for 22 … rules. But here is a typical sample of growth rules (note that different rules are run for different numbers of steps to achieve a roughly balanced level of detail):

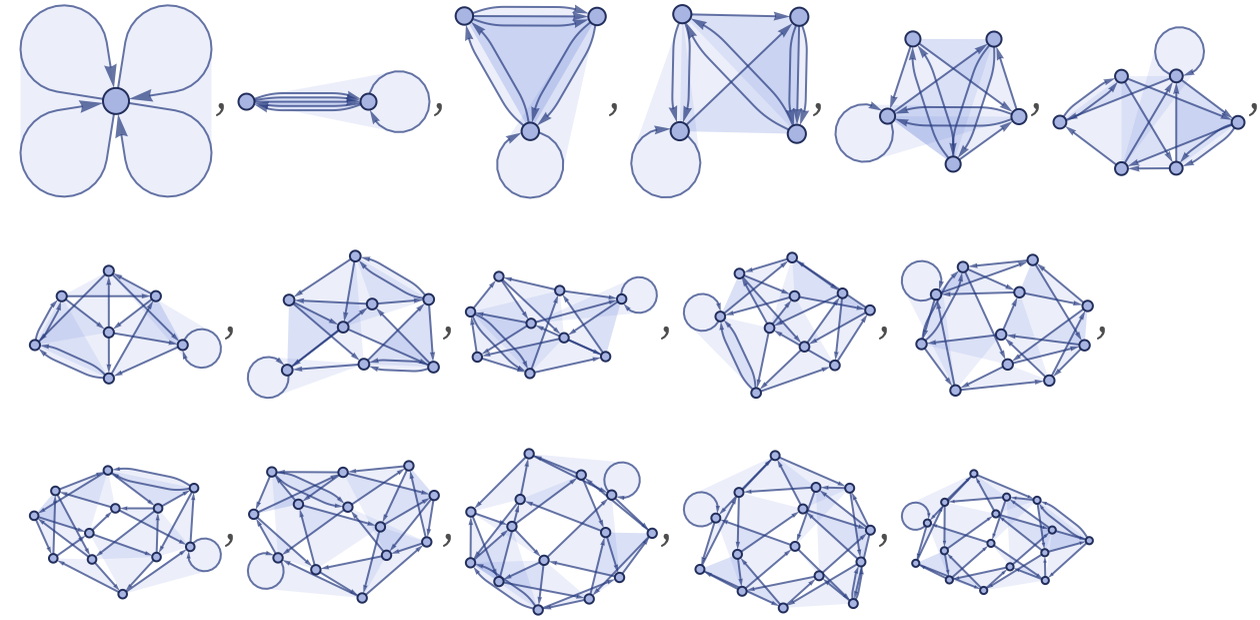
And even though there are only 3 relations on the right-hand side (rather than the 4 in 22 42) these rules can produce globular structures. Some examples are:
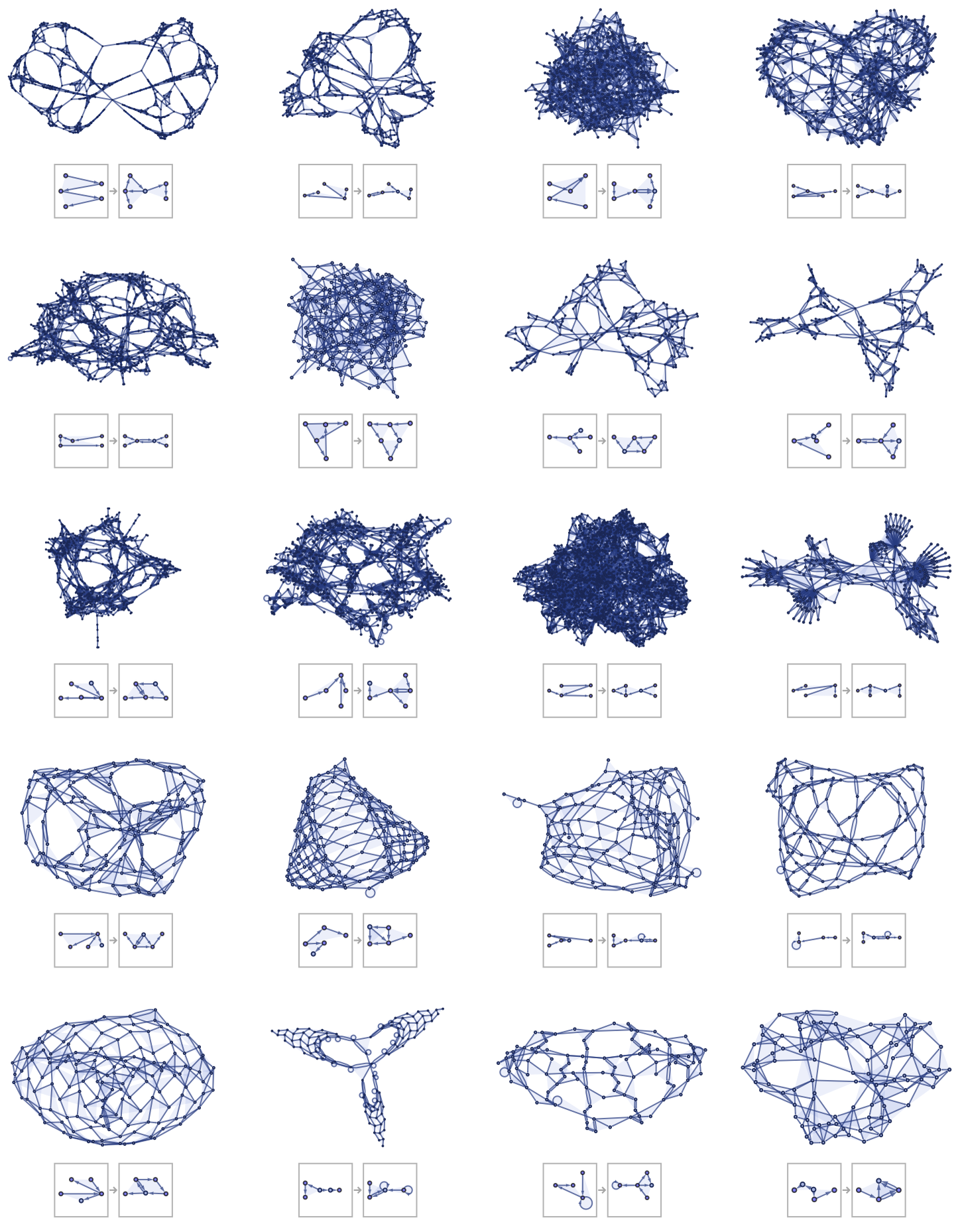
A new phenomenon exhibited by 23 33 rules is the formation of globular structures by what amounts to slow grow. This is exemplified by a rule like:
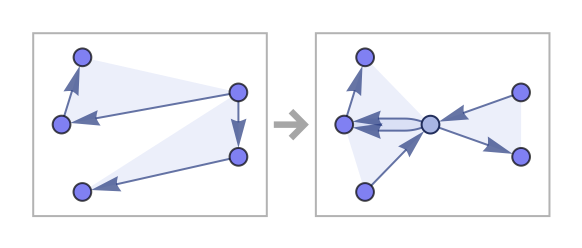
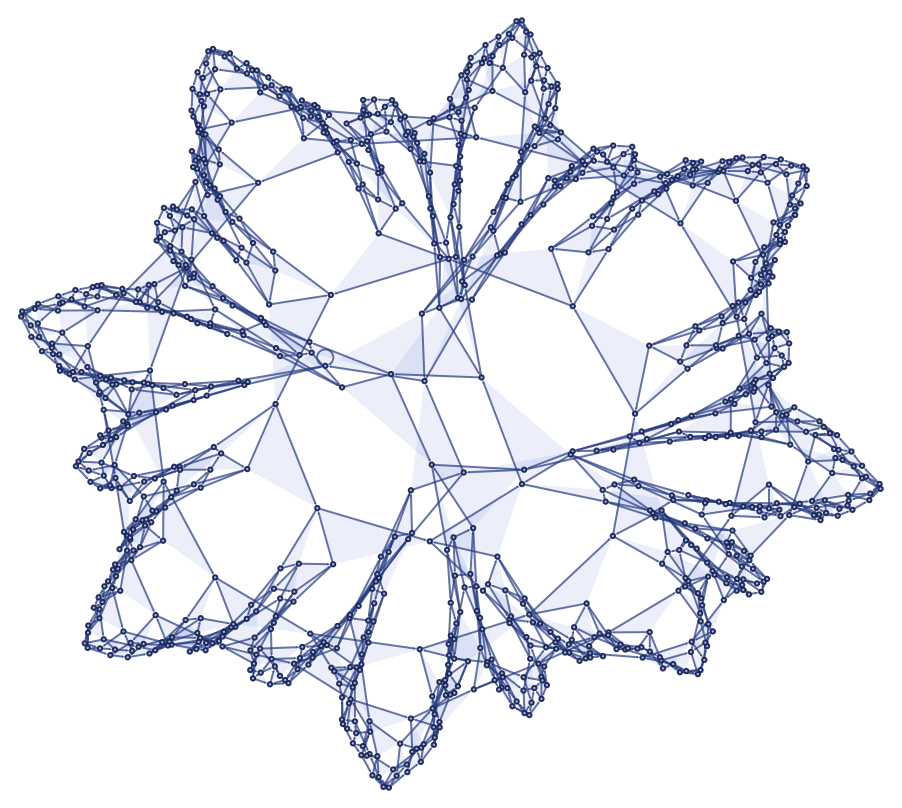
This rule progressively builds up a structure by growing only in one place at a time (the position of the surviving self-loop):
After 1000 steps the rule has produced this structure containing 1000 ternary relations (plus the 2 already present in the initial condition):
Another example of slow growth occurs in the rule
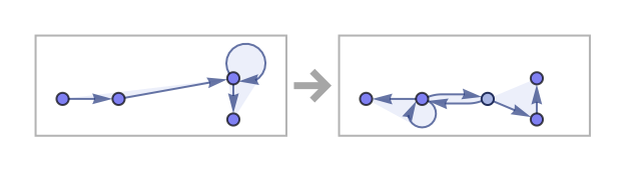
which after 1000 steps generates:

Note the presence here of regions of square grids. These occur even more prominently in the rule
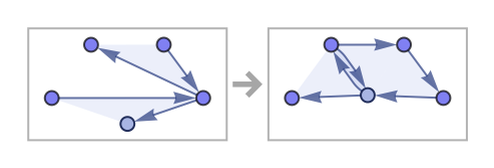
which after 500 steps produces:
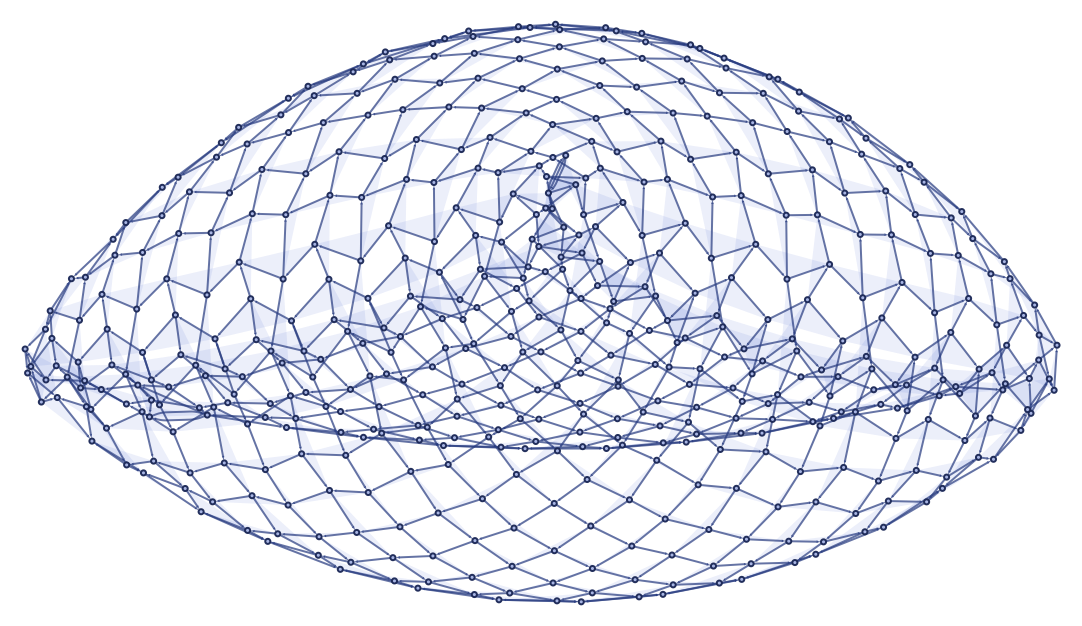
As we will discuss in the next section, the grid here becomes quite explicit when the hypergraph is rendered in 3D. Notice that the grid is not evident even after 20 steps in the evolution of the rule; it takes longer to emerge:

Once again, though, the rule adds just a single relation at each generation; in effect the grid is being “knitted” one node at a time.
The emergence of a grid is still easier to see in the rule
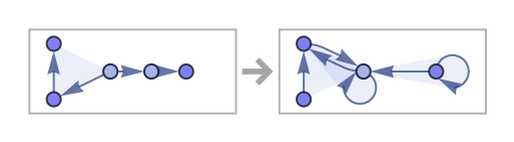
which after 200 steps yields:
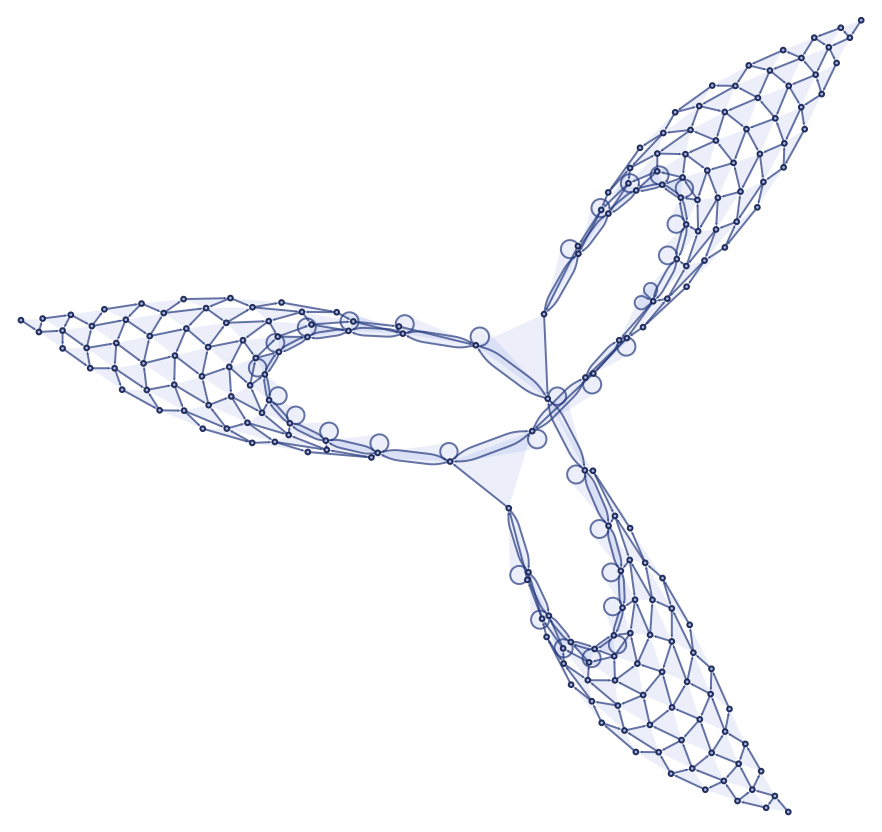
Once again, the “knitting” of this form is far from obvious in the first 20 steps of evolution:

Just sometimes, however, the behavior is quite easy to trace, as in this particularly direct example of “knitting”
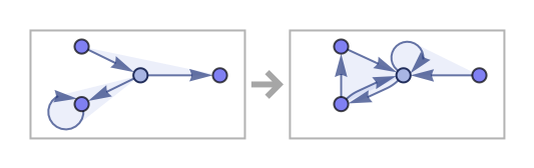
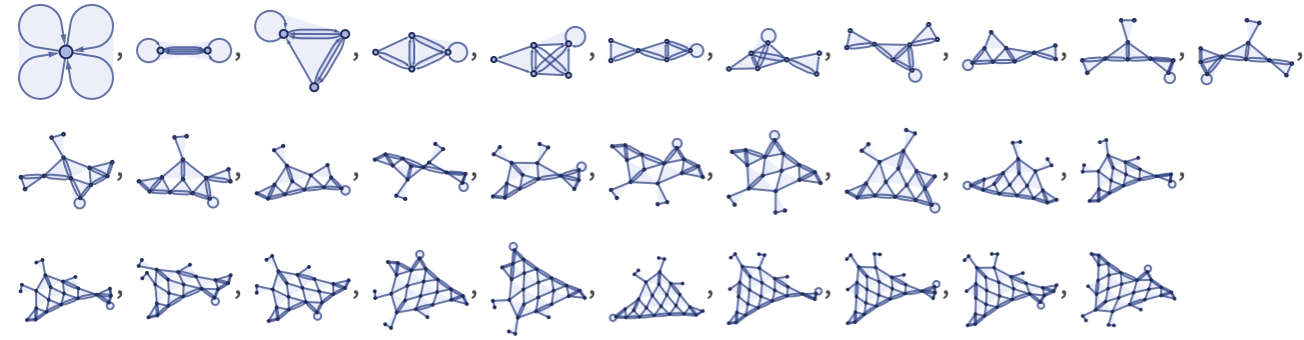
which after 200 steps yields:
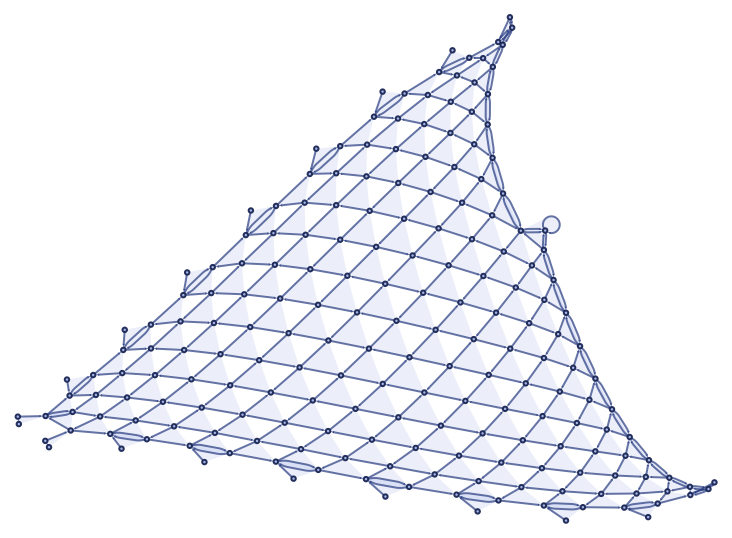
As a different example of slow growth, consider the rule:
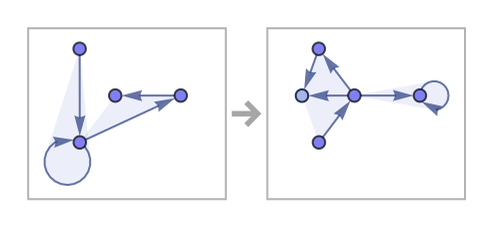
After 200 steps this rule gives
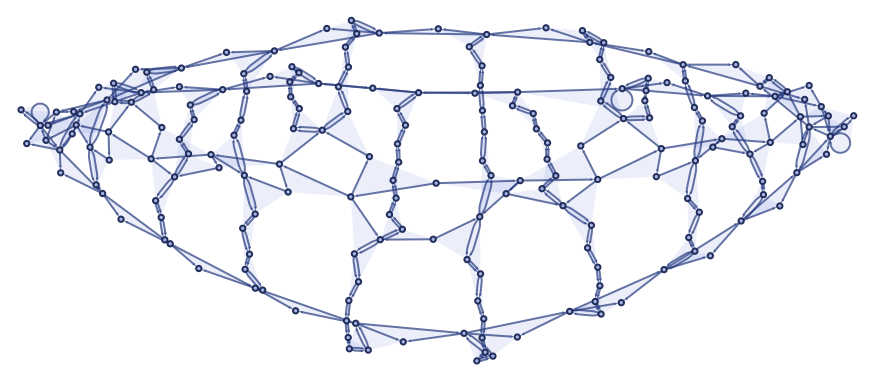
while after 500 steps it gives:
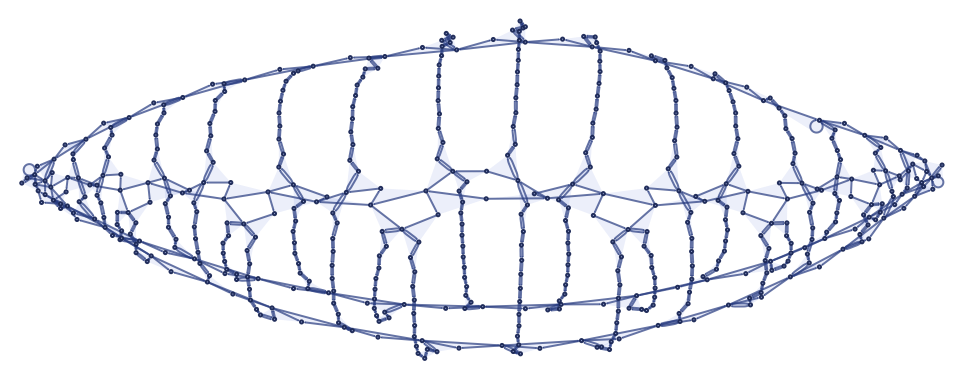
Looking at all 79 million or so 23 33 rules in canonical order, one finds that rules with slow growth are quite rare and are strongly localized to about 10 broad regions in the space of possible rules. Of rules with slow growth, only a few percent form nontrivial globular structures. And of these, perhaps 10% exhibit obvious lattice-like patterns.
The pictures below show additional examples. Note that—as we will discuss later—many of the patterns here are best visualized in 3D.
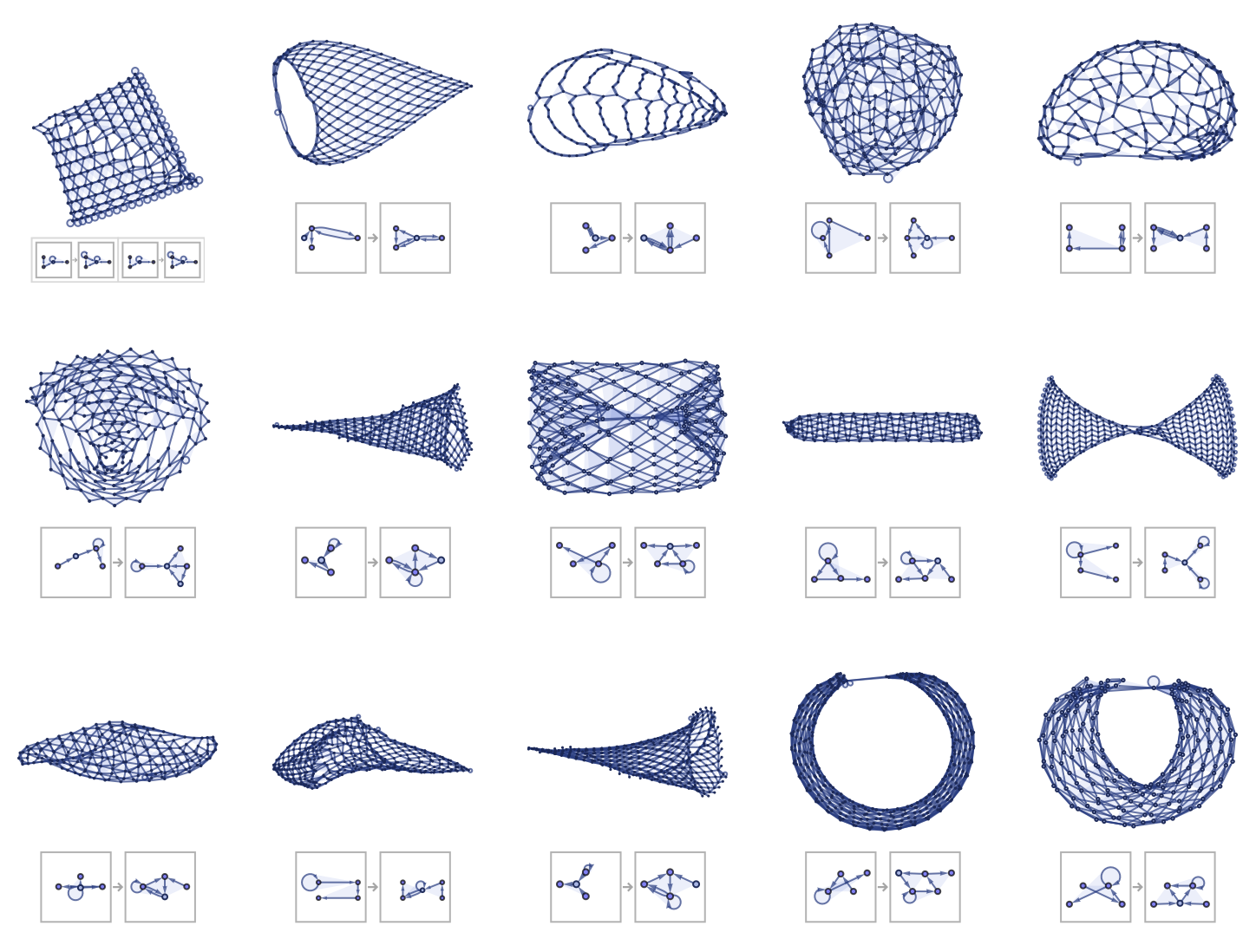
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review