We have formulated our models in terms of the rewriting of collections of relations between elements. And in this formulation, we might represent a state in one of our models as a list of (here 3-ary) relations
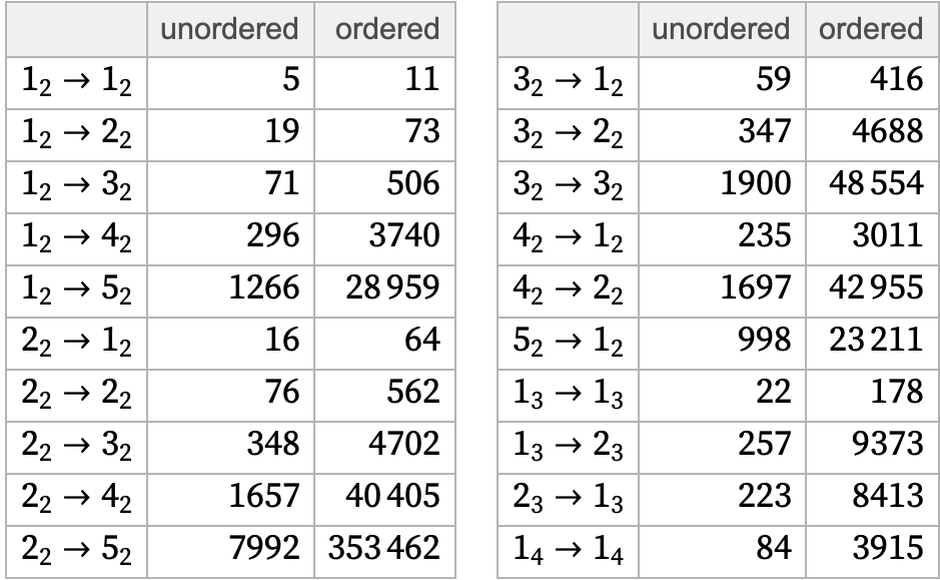
and the rule for the model as
where x, y, ... are taken to be pattern or quantified variables, suggesting notations like [98]
or [99]:
An alternative to these kinds of symbolic representations is to think—as we have often done here—in terms of transformations of directed hypergraphs. The state of one of our models might then be represented by a directed hypergraph such as
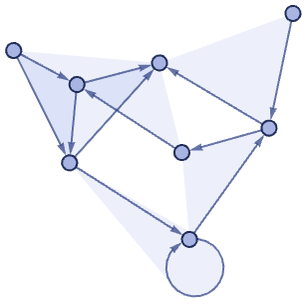
while the rule would be:
But in an effort to understand the generality of our models—as well as to see how best to enumerate instances of them—it is worthwhile to consider alternative formulations.
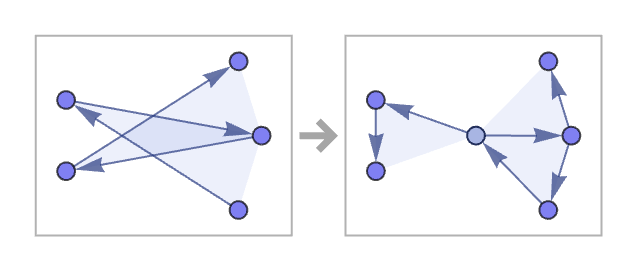
One possibility to consider is ordinary graphs. If we are dealing only with binary relations, then our models are immediately equivalent to transformations of directed graphs.
But if we have general k-ary relations in our models, there is no immediate equivalence to ordinary graphs. In principle we can represent a k-ary hyperedge (at least for k > 0) by a sequence of ordinary graph edges:
For the hypergraph above, this then yields:

The rule above can be stated in terms of ordinary directed graphs as:
In terms of hypergraphs, the result of 5 and 10 steps of evolution according to this rule is
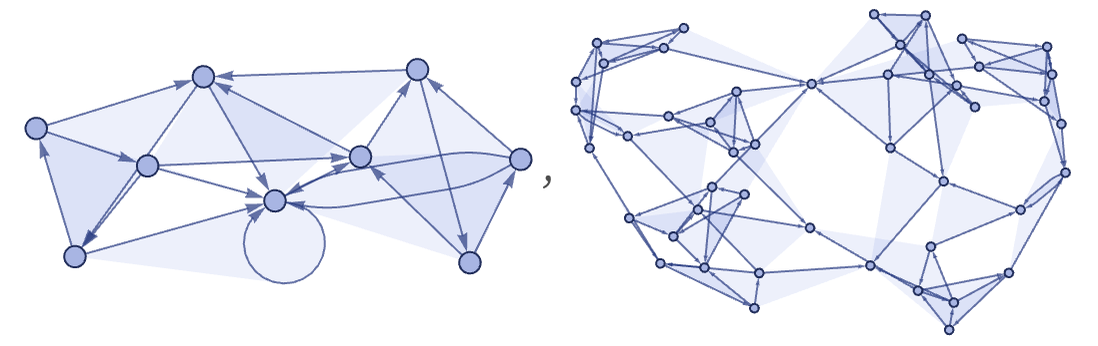
and the corresponding result in terms of ordinary directed graphs is:
In thinking about ordinary graphs, it is natural also to consider the undirected case. And indeed—as was done extensively in [1:9]—it is possible to study many of the same things we do here with our models also in the context of undirected graphs. However, transformations of undirected graphs lack some of the flexibility and generality that exist in our models based on directed hypergraphs.
It is straightforward to convert from a system described in terms of undirected graphs to one described using our models: just represent each edge in the undirected graph as a pair of directed binary hyperedges, as in:
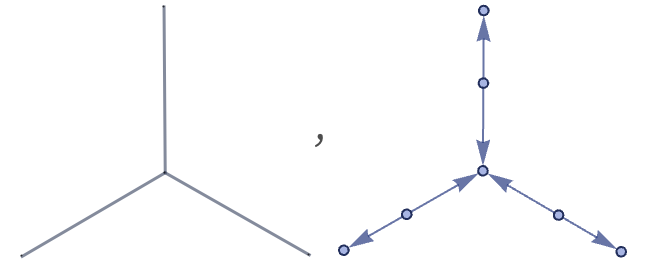
Transformations of undirected graphs work the same—though with paired edges. So, for example, the rule
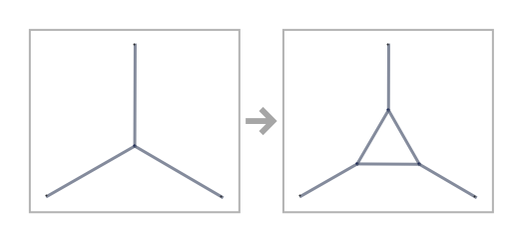
becomes
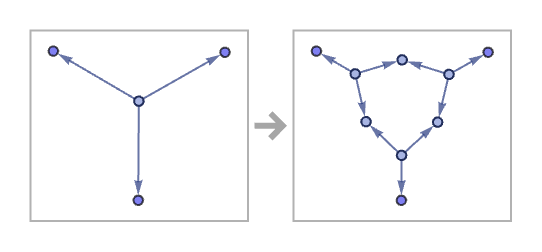
which yields:
In dealing with undirected graphs—as in [1:9]—it is natural to make the further simplification that all graphs are trivalent (or “cubic”). In the context of ordinary graphs, nothing is lost by this assumption: any higher-valence node can always be represented directly as a combination of trivalent nodes. But the point about restricting to trivalent graphs is that it makes the set of possible rules better defined—because without this restriction, one can easily end up having to specify an infinite family of rules to cover graphs of arbitrary valence that are generated. (In our models based on transformations for arbitrary relations, no analogous issue comes up.)
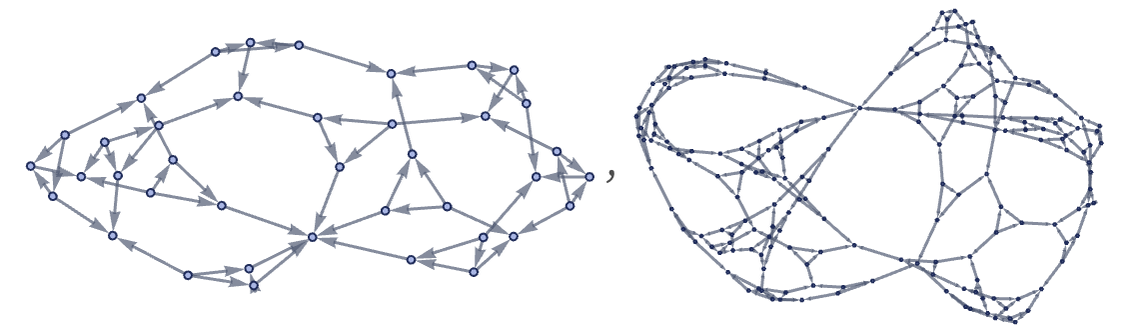
It is particularly easy to get intricate nested structures from rules based on undirected trivalent graphs; it is considerably more difficult to get more complex behavior:
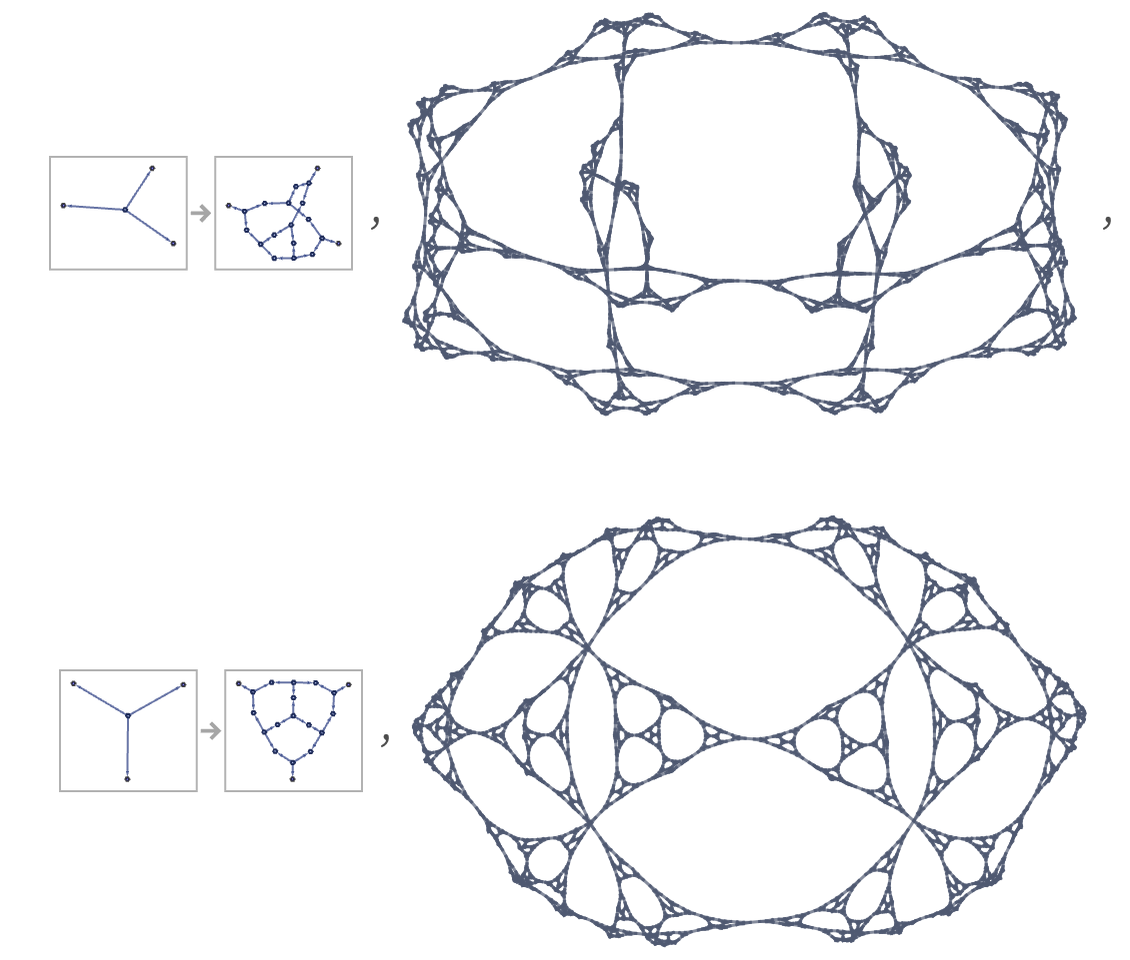
Another issue in models based on undirected graphs has to do with the fact that the objects that appear in their transformation rules do not have exactly the same character as the objects on which they act. In our hypergraph-based models, both sides of a transformation are collections of relations (that can be represented by hypergraphs)—just like what appears in the states on which these transformations act. But in models based on undirected graphs, what appears in a transformation is not an ordinary graph: instead it is a subgraph with “dangling connections” (or “half-edges”) that must be matched up with part of the graph on which the transformation acts.
Given this setup, it is then unclear, for example, whether or not the rule above—stated in terms of undirected graphs—should be considered to match the graph:

(In a sense, the issue is that while our models are based on applying rules to collections of complete hyperedges, models based on undirected graphs effectively apply rules to collections of nodes, requiring “dangling connections” to be treated separately.)
Another apparent problem with undirected trivalent graphs is that if the right-hand side of a transformation has lower symmetry than the left-hand side, as in
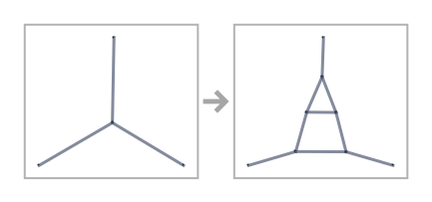
then it can seem “undefined” how the right-hand side should be inserted into the final graph. Having seen our models here, however, it is now clear that this is just one of many examples where multiple different updates can be applied, as represented by multiway systems.
A further issue with systems based on undirected trivalent graphs has to do with the enumeration of possible states and possible rules. If a graph is represented by pairs of vertices corresponding to edges, as in
the fact that the graph is trivalent in a sense corresponds to a global constraint that each vertex must appear exactly three times. The alternate “vertex-based” representation
does not overcome this issue. In our models based on collections of relations, however, there are no such global constraints, and enumeration of possible states—and rules—is straightforward. (In our models, as in trivalent undirected graphs, there is, however, still the issue of canonicalization.)
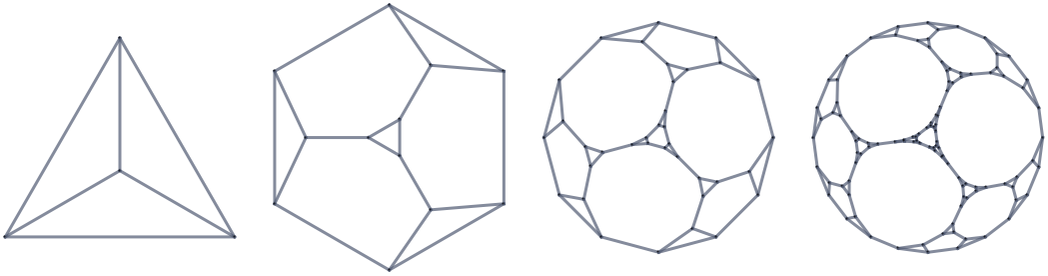
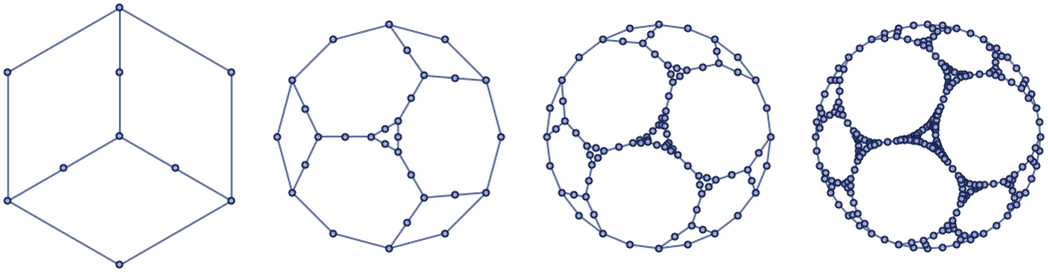
In the end, though, it is still perfectly possible to enumerate distinct trivalent undirected graphs (here dropping cases with self-loops and multiple edges)
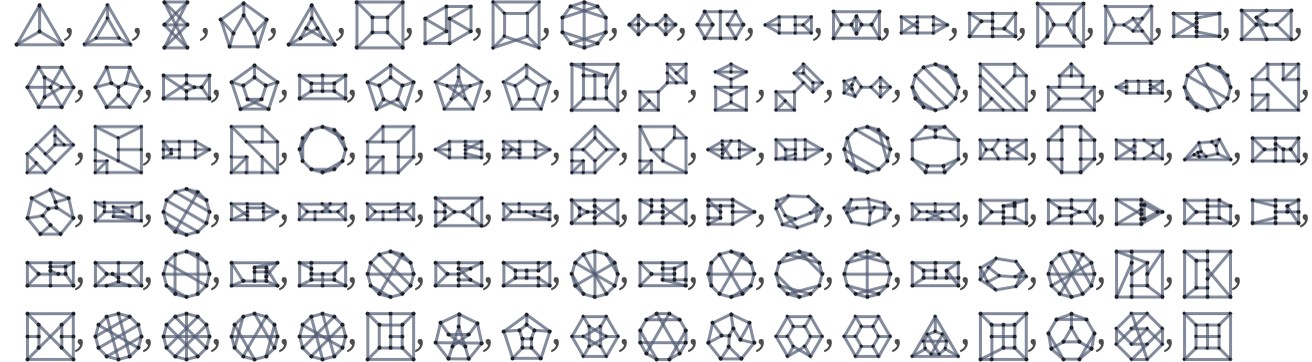
as well as rules for transforming them, and indeed to build up a rich analysis of their behavior [1:9.12]. Notions such as causal invariance are also immediately applicable, and for example one finds that the simplest subgraphs that do not overlap themselves, and so guarantee causal invariance, are [1:p515][87]:
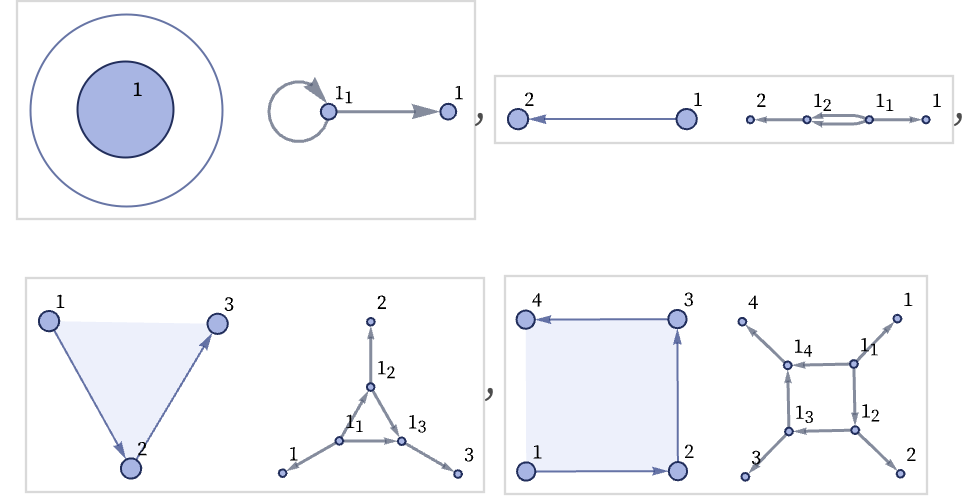
Directed graphs define an ordering for every edge. But it is also possible to have ordered graphs in which the individual edges are undirected, but an order is defined for the edges at any given vertex [87]. Trivalent such ordered graphs can be represented by collections of ordered triples, where each triple corresponds to a vertex, and each number in each triple specifies the destination in the whole list of a particular edge:
For visualization purposes one can “name” each element of each triple by a color
and then the ordered graph can be rendered as:

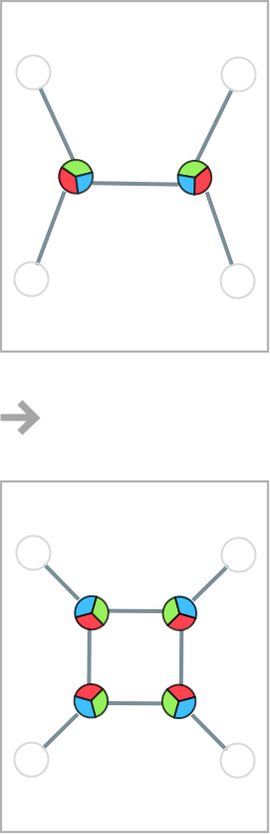
In the context of our models, an ordered trivalent graph can immediately be represented as a hypergraph with ternary hyperedges corresponding to the trivalent nodes, and binary hyperedges corresponding to the edges that connect these nodes:
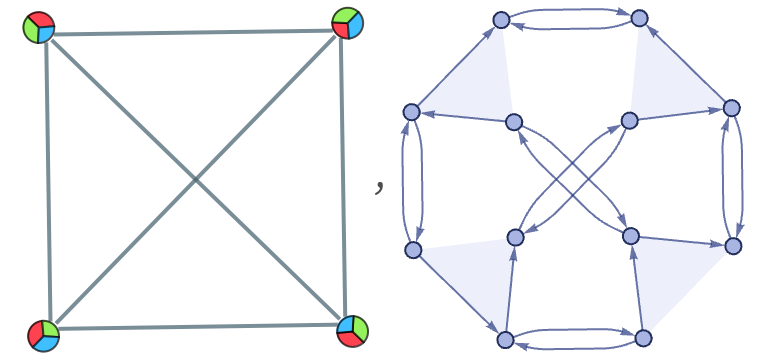
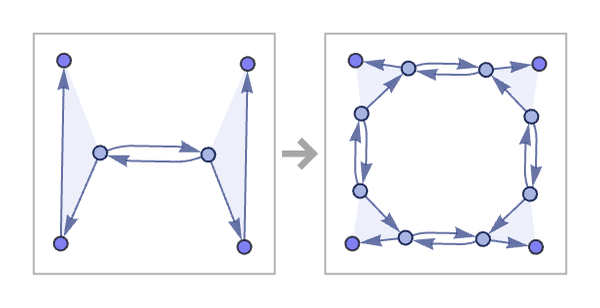
To give rules for ordered trivalent graphs, one must specify how to transform subgraphs with “dangling connections”. Given the rule (where letters represent dangling connections)
the evolution of the system is:
The corresponding rule for hypergraphs would be
and the corresponding evolution is:
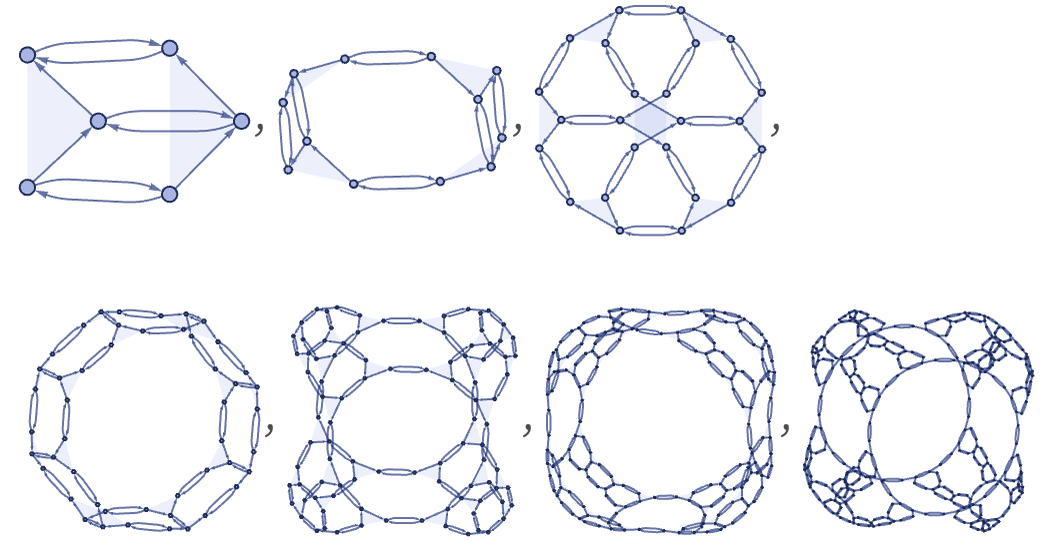
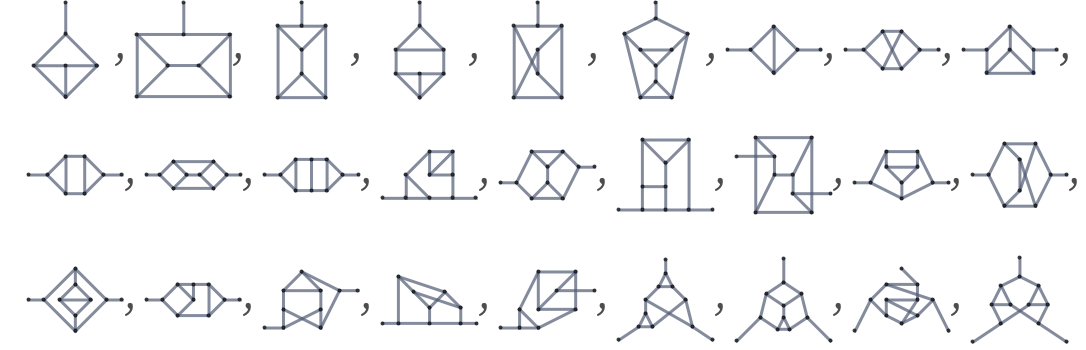
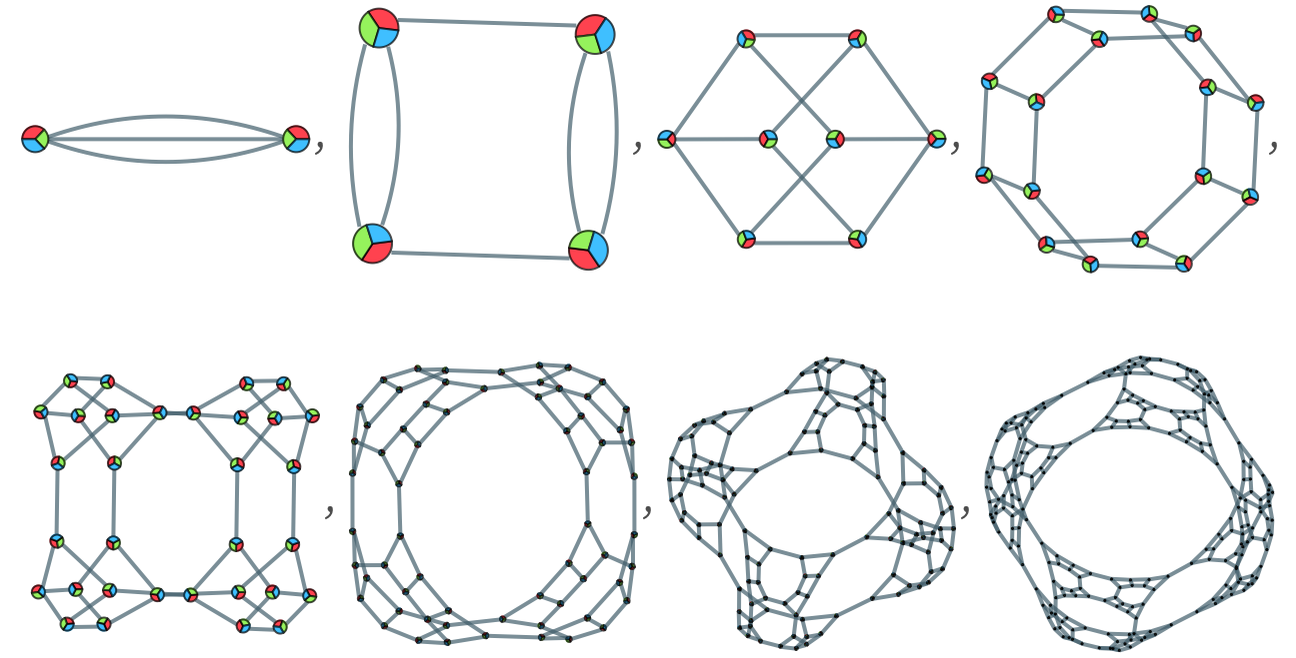
The rule just shown is example of a rule with 2 4 internal nodes and 4 dangling connections—which is the smallest class that supports growth from minimal initial conditions. There are altogether 264 rules of this type, with rules of the following forms (up to vertex orderings) [87]:

These rules produce the following distinct outcomes:
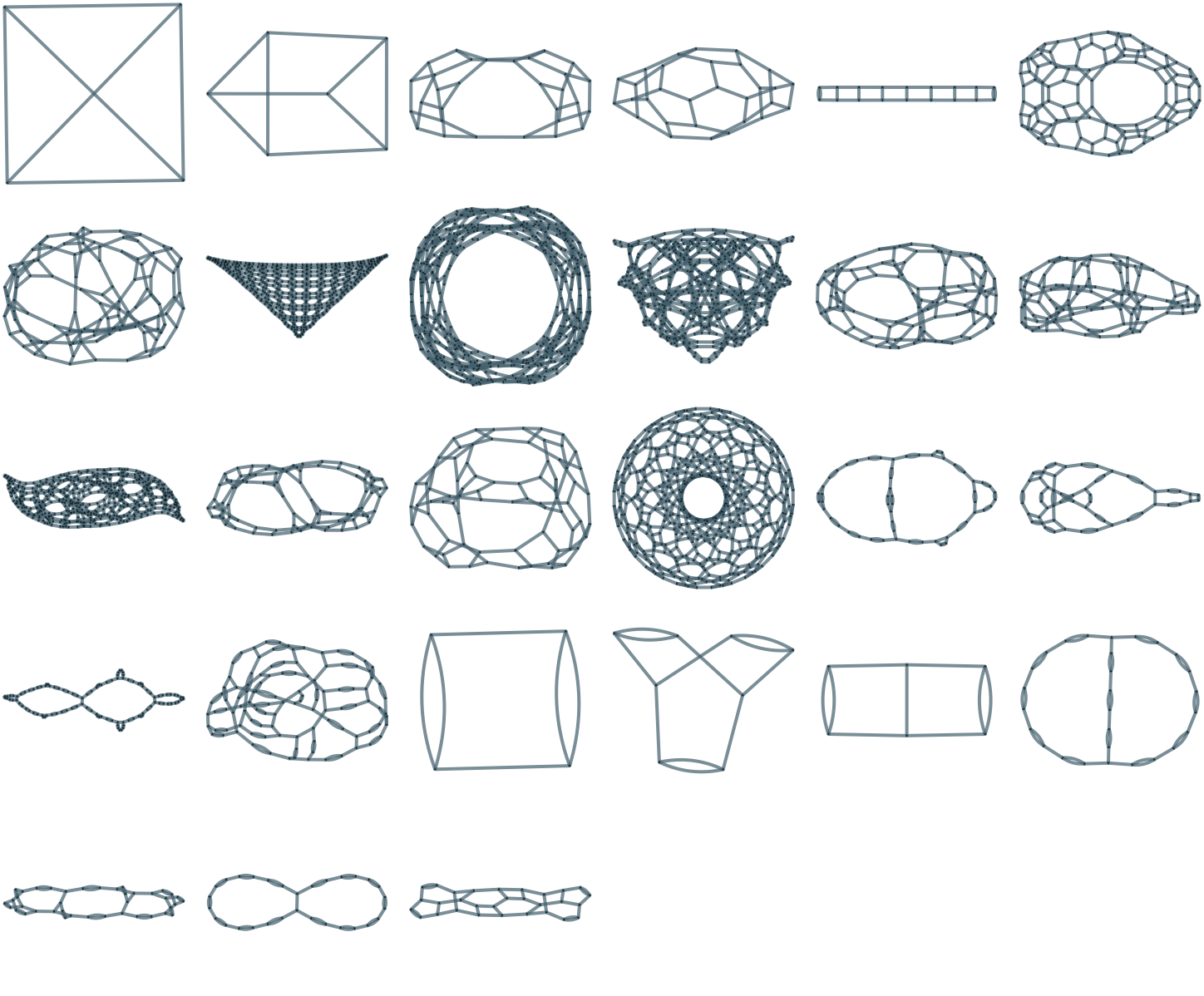
Even though there is a direct translation between ordered trivalent graphs and our models, what is considered a simple rule (for example for purposes of enumeration) is different in the two cases. And while it is more difficult to find valid rules with ordered trivalent graphs, it is notable that even some of the very simplest such rules generate structures with limiting manifold features that we see only after exploring thousands of rules in our models:
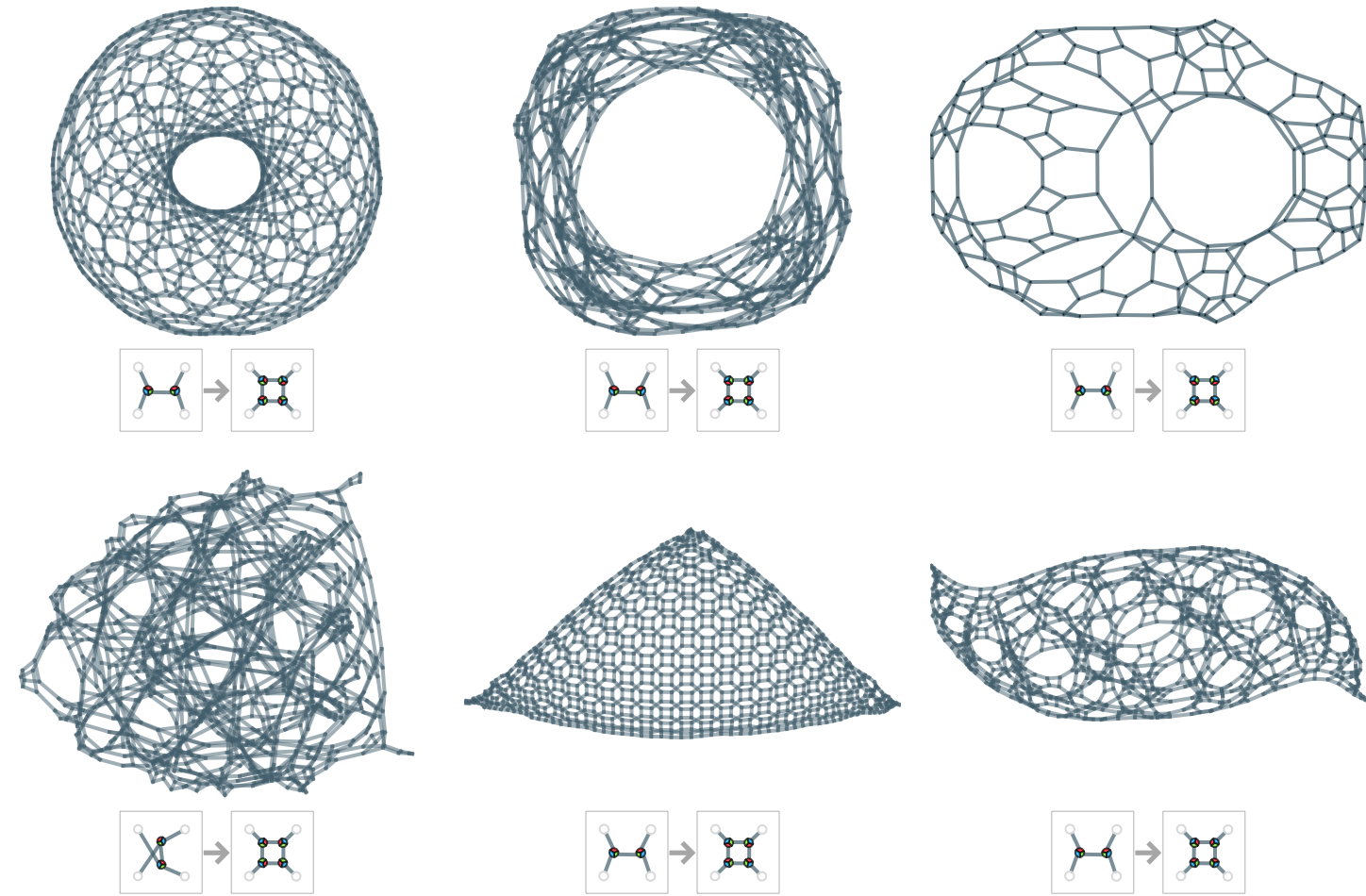
Our models are based on directed (or ordered) hypergraphs. And although the notion is not as natural as for ordinary graphs, one can also consider undirected (or unordered) hypergraphs, in which all elements in a hyperedge are in effect unordered and equivalent. (In general one can also imagine considering any specific set of permutations of elements to be equivalent.)
For unordered hypergraphs one can still use a representation like
but now there are no arrows needed within each hyperedge:
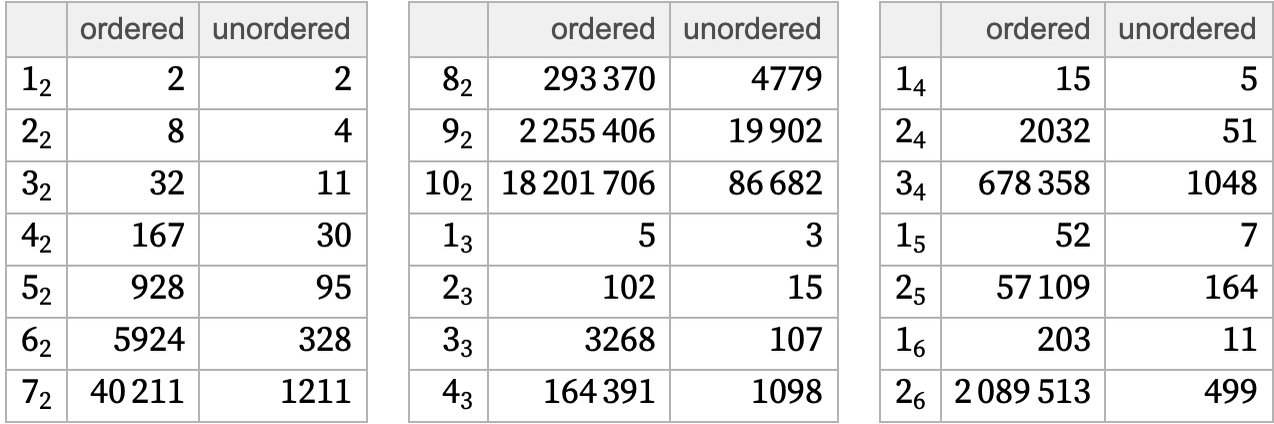
There are considerably fewer unordered hypergraphs with a given signature than ordered ones:
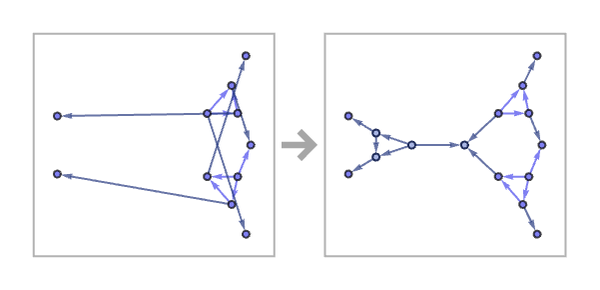
There is a translation between unordered hypergraphs and ordered ones, or specifically between unordered hypergraphs and directed graphs. Essentially one creates an incidence graph in which each node and each hyperedge in the unordered hypergraph becomes a node in the directed graph—so that the unordered hypergraph above becomes:
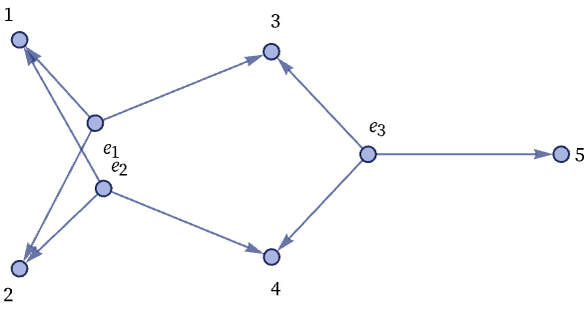
But despite this equivalence, just as in the case of ordered graphs, the sequence of rules will be different in an enumeration based on unordered hypergraphs from one based on ordered hypergraphs.
There are many fewer rules with a given signature for unordered hypergraphs than for ordered ones:
Here is an example of a 23 33 rule for unordered hypergraphs:
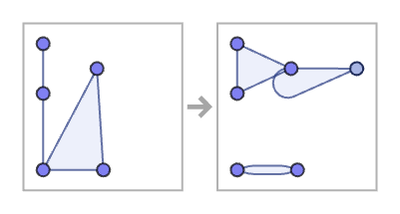
Starting from an unordered double ternary self-loop, this evolves as:
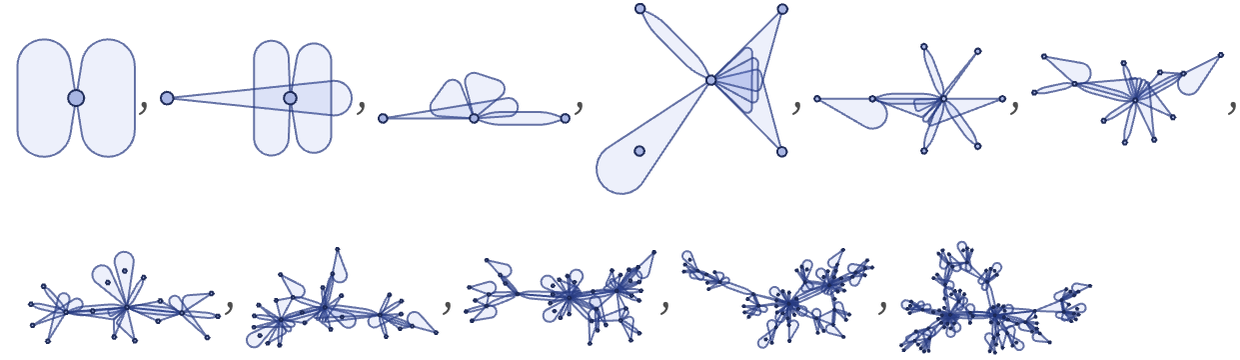
In general the behavior seen for unordered rules with a given signature is considerably simpler than for ordered rules with the same signature. For example, here is typical behavior seen with a random set of unordered 23 33 rules:
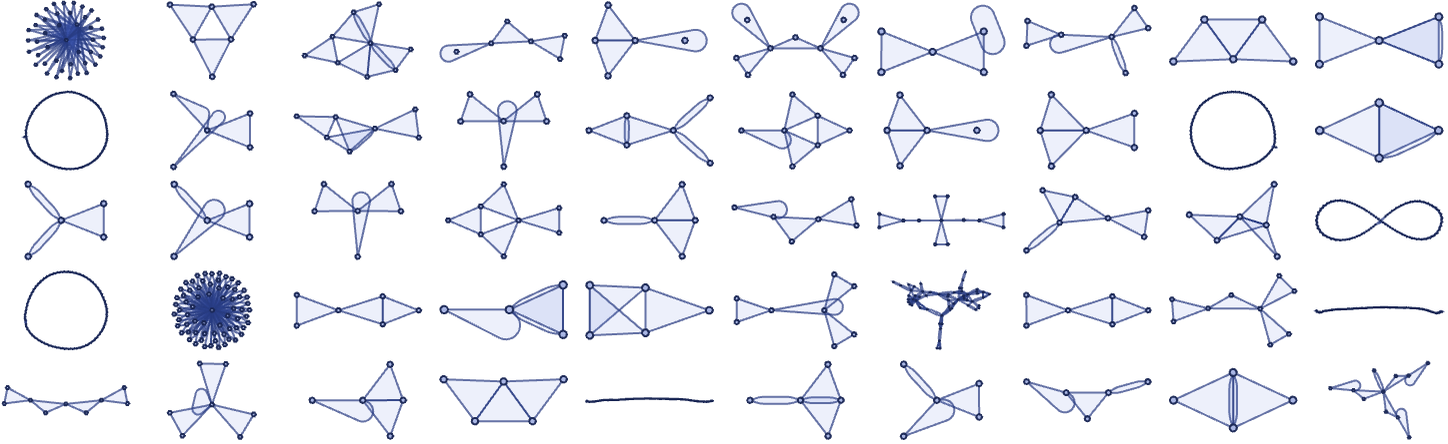
In ordered 23 33 rules, globular structures are quite common; in the unordered case they are not. Once one reaches 23 43 rules, however, globular structures become common even for unordered hypergraph rules:

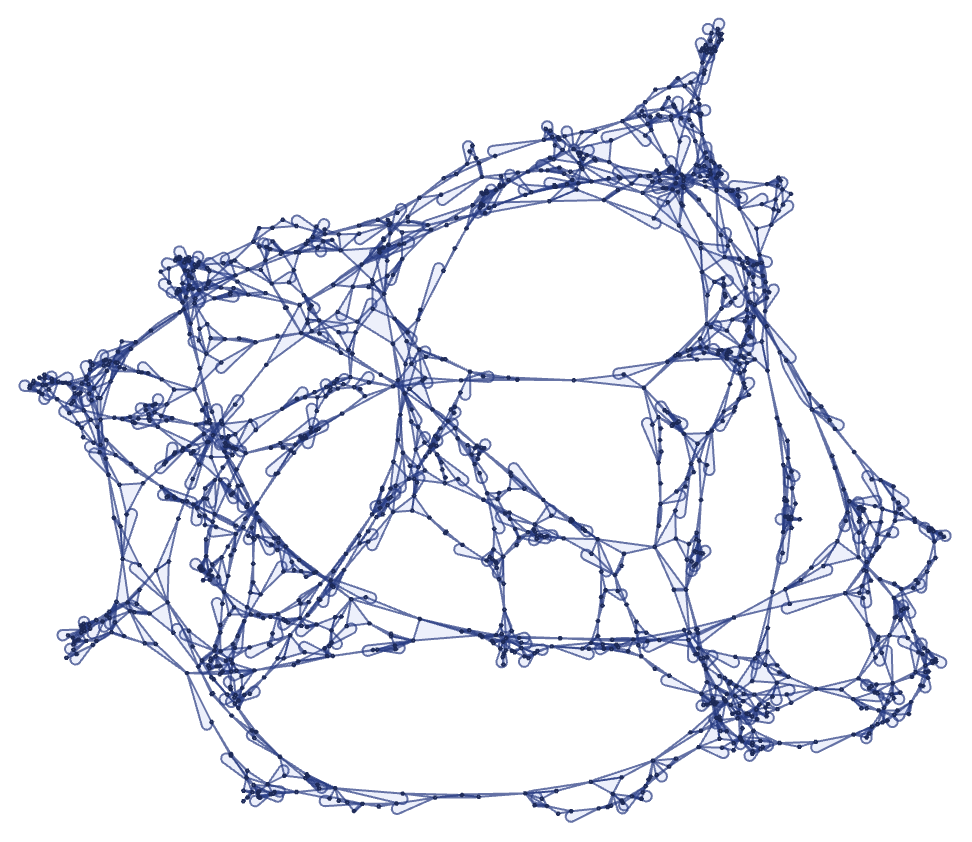
It is worth noting that the concept of unordered hypergraphs can also be applied for binary hyperedges, in which case it corresponds to undirected ordinary graphs. We discussed above the specific case of trivalent undirected graphs, but one can also consider enumerating rules that allow any valence.
An example is
which evolves from an undirected double self-loop according to:
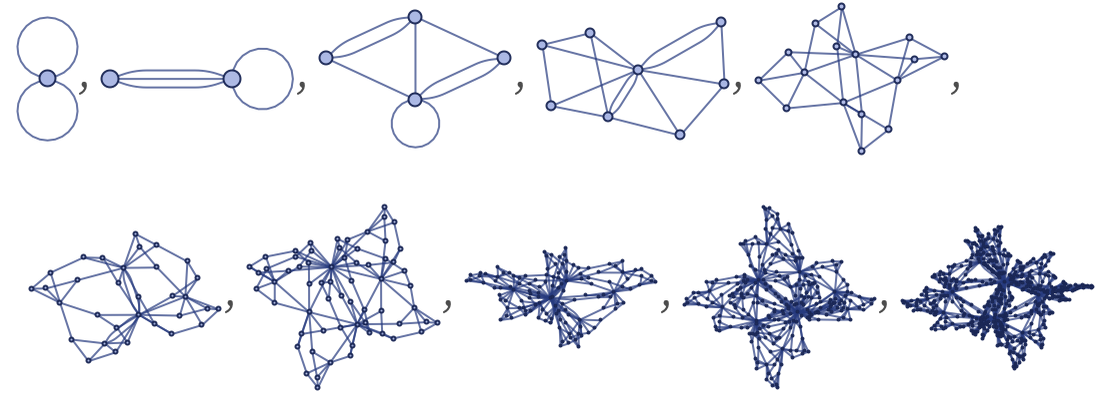
This rule is similar, but not identical, to a rule we have often used as an example:
Interpreting this rule as referring to undirected graphs, it evolves according to:
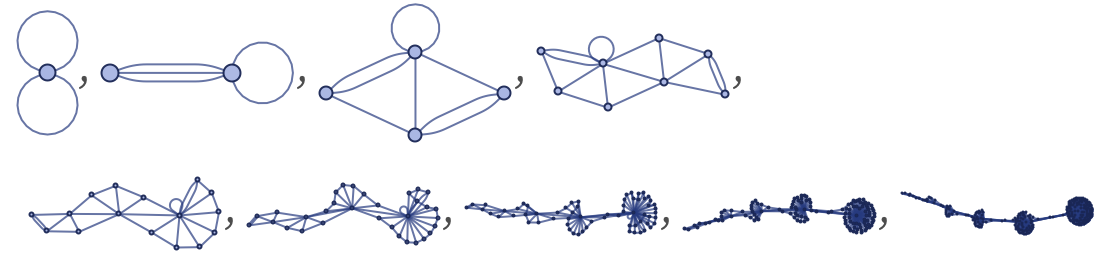
In general, rules for undirected graphs of a given signature yield significantly simpler behavior than rules of the same signature for directed graphs. And, for example, even among all the 7992 distinct 22 52 rules for undirected graphs, no globular structures are seen.
Hypergraphs provide a convenient approach to representing our models. But there are other approaches that focus more on the symbolic structure of the models. For example, we can think of a rule such as
as defining a transformation for expressions involving a ternary operator f together with a commutative and associative (n-ary) operator ∘:
In this formulation, the ∘ operator can effectively be arbitrarily nested. But in the usual setup of our models, f cannot be nested. One could certainly imagine a generalization in which one considers (much as in [98]) transformations on symbolic expressions with arbitrary structures, represented by pattern rules like
or even:
And much as in the previous subsection, it is always possible to represent such transformations in our models, for example by having fixed subhypergraphs that act as “markers” to distinguish different functional heads or different “types”. (Similar methods can be used to have literals in addition to pattern variables in the transformations, as well as “named slots” [100].)
Our models can be thought of as abstract rewriting (or reduction) systems that operate on hypergraphs, or general collections of relations. Frameworks such as lambda calculus [101][102] and combinatory logic [103][104] have some similarities, but focus on defining reductions for tree structures, rather than general graphs or hypergraphs.
One can ask how our models relate to traditional mathematical systems, for example from universal algebra [105][106]. One major difference is that our models focus on transformations, whereas traditional axiomatic systems tend to focus on equalities. However, it is always possible to define two-way rules or pairs of rules XY, YX which in effect represent equalities, and on which a variety of methods from logic and mathematics can be used.
The general case of our models seems to be somewhat out of the scope of traditional mathematical systems. However, particularly if one considers the simpler case of string substitution systems, it is possible to see a variety of connections [1:p938]. For example, two-way string rewrites can be thought of as defining the relations for a semigroup (or, more specifically, a monoid). If one adds inverse elements, then one has a group.
One thinks of the strings as corresponding to words in the group. Then the multiway evolution of the system corresponds to starting with particular words and repeatedly applying relations to them—to produce other words which for the purposes of the group are considered equivalent.
This is in a sense a dual operation to what happens in constructing the Cayley graph of a group, where one repeatedly adds generators to words, always reducing by using the relations in the group (see 4.17).
For example, consider the multiway system defined by the rule:
The first part of the multiway (states) graph associated with this rule is:
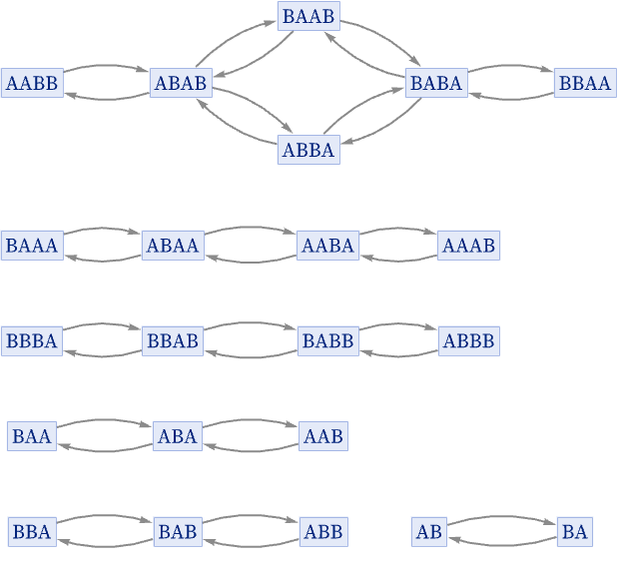
Ignoring inverse elements (which in this case just make double edges) the first part of the infinite Cayley graph for the group with relations ABBA has the form:
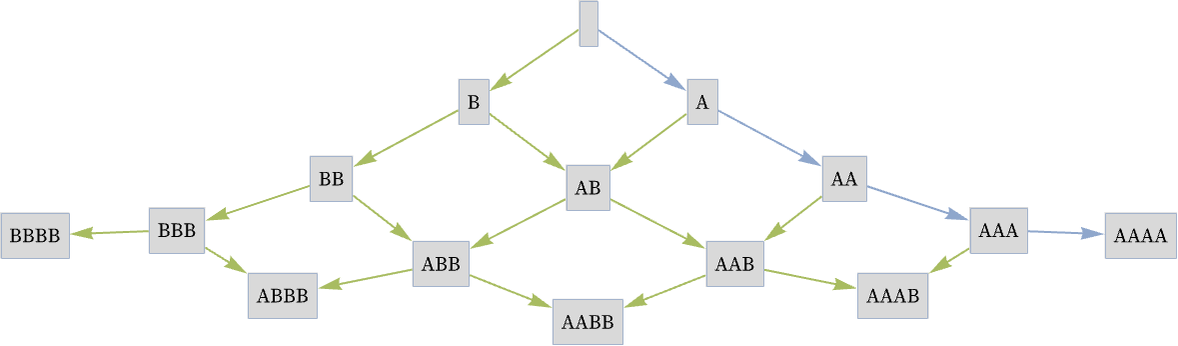
One can think of the Cayley graph as being created by starting with a tree, corresponding to the Cayley graph for a free group, then identifying nodes that are related by relations. The edges in the multiway graph (which correspond to updating events) thus have a correspondence to cycles in the Cayley graph.
As one further example, consider the (finite) group S3 which can be thought of as being specified by the relations:
The Cayley graph in this case is simply:
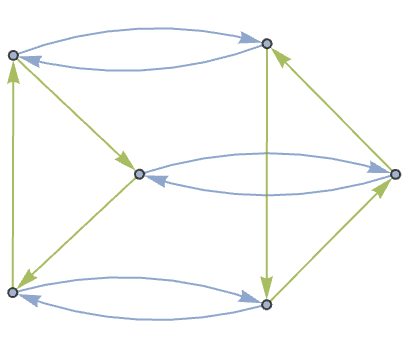
The multiway graph in this case begins:
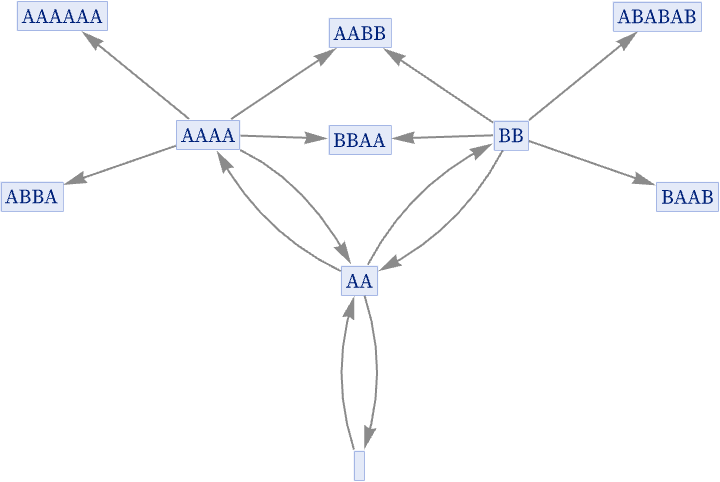
Continuing for a few more steps gives:

On successive steps, the volumes Σt in these multiway graphs grow like:
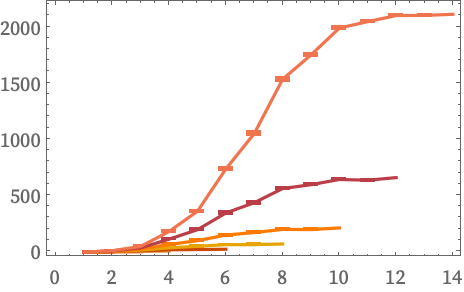
There does not appear to be any direct correspondence to quantities such as growth rates of Cayley graphs (cf. [22]).
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review