8.12 Basic Concepts of Quantum Mechanics

Quantum mechanics is a key known feature of physics, and also, it seems, a natural and inevitable feature of our models. In classical physics—or in a system like a cellular automaton—one basically has rules that specify a unique path of history for the evolution of a system. But our models are not set up to define any such unique path of history. Instead, the models just give possible rewrites that can be performed on hypergraphs—but they do not say when or where these rewrites should be applied. So this means that—like the formalism of quantum mechanics—our models in a sense allow many different paths of history.

There is, however, ultimately nothing non-deterministic about our models. Although they allow many different sequences of updating events—each of which can be viewed as a different path of history—the models still completely determine the overall set of possible sequences of updating events. And indeed at a global level, everything about the model can be captured in a multiway graph [1:5.6]—like the one below—with nodes in the graph corresponding to states of the system (here, for simplicity, a string substitution system), and every possible path through the graph corresponding to a possible history.

In the standard formalism of quantum mechanics, one usually just imagines that all one can determine are probabilities for different histories or different outcomes. But this has made it something of a mystery why we have the impression that a definite objective reality seems to exist. One possible explanation would be that at some level a branch of reality exists for every possible behavior, and that we just experience the branch that our thread of consciousness has happened to follow.

But our models immediately suggest another, more complete, and arguably much more scientifically satisfying, possibility. In essence, they suggest that there is ultimately a global objective reality, defined by the multiway system, and it is merely the locality of our experience that causes us to describe things in terms of probabilities, and all the various detailed features of the standard formalism of quantum mechanics.

We will proceed in two stages. First, we will discuss the notion of an observer in the context of multiway systems, and the relation of this to questions about objective reality. And having done this, we will be in a position to discuss ideas like quantum measurement, and the role that causal invariance turns out to play in allowing observers to experience definite, seemingly classical results.

So how might we represent a quantum observer in our models? The first key point is that the observer—being part of the universe—must themselves be a multiway system. And in addition, everything the observer does—and experiences—must correspond to events that occur in the model.

This latter point also came up when we discussed spacetime—and we concluded there that it meant we only needed to consider the graph of causal relationships between events. To characterize any given observer, we then just had to say how the observer would sample this causal graph. A typical example in studying spacetime is to consider an observer in an inertial reference frame—which corresponds to a particular foliation of the causal graph. But in general to characterize what any observer will experience in the course of time, we need some sequence of spacelike hypersurfaces that form a foliation which respects the causal relationships—and thus the ordering relations between events—defined by the causal graph.

But now we can see an analog of this in the quantum mechanical case. However, instead of considering foliations of the causal graph, what we need to consider now are foliations of the multiway graph:

In the course of time, the observer progresses through such a foliation, in effect at each step observing some collection of states, with certain relationships between them. A different observer, however, might want to sample the states differently, and might effectively define a different foliation.

One can potentially think of a different foliation as being a different “quantum observation frame” or “quantum frame”, analogous to the different reference frames one considers in studying spacetime. In the case of something like an inertial frame, one is effectively defining how an observer will sample different parts of space over the course of time. In a quantum observation frame one might have a more elaborate specification, involving sampling particular states of relevance to some measurement or another. But the key point is that a quantum observer can in principle use any quantum observation frame that corresponds to a foliation that respects the relationships between states defined by the multiway graph (and thus has a meaningful notion of time).

In both the spacetime case and the quantum case, the slices in the foliation are indexed by time. But while in the spacetime case, where each slice corresponds to a spacelike hypersurface that spans ordinary space, in the quantum case, each slice corresponds to what we can call a branchlike hypersurface that spans not ordinary space, but instead the space of states, or the space of branches in the multiway system. But even without knowing the details of this space, we can already come to some conclusions.

In particular, we can ask what observers with different quantum observation frames—and thus different choices of branchlike hypersurfaces—will conclude about relationships between states. And the point is that so long as the foliations that are used respect the orderings defined by the multiway graph, all observers must inevitably come to the same conclusions about the structure of the multiway graph—and therefore, for example, the relationships between states. Different observers may sample the multiway graph differently, and experience different histories, but they are always ultimately sampling the same graph.

One feature of traditional quantum formalism is its concept of making measurements that effectively reduce collections of states—as exist in a multiway system—to what is basically a single state analogous to what would be seen in a classical single path of evolution. From the point of view of quantum observation frames, one can think of such a measurement as being achieved by sculpting the quantum observation frame to effectively pick out a single state in the multiway system:

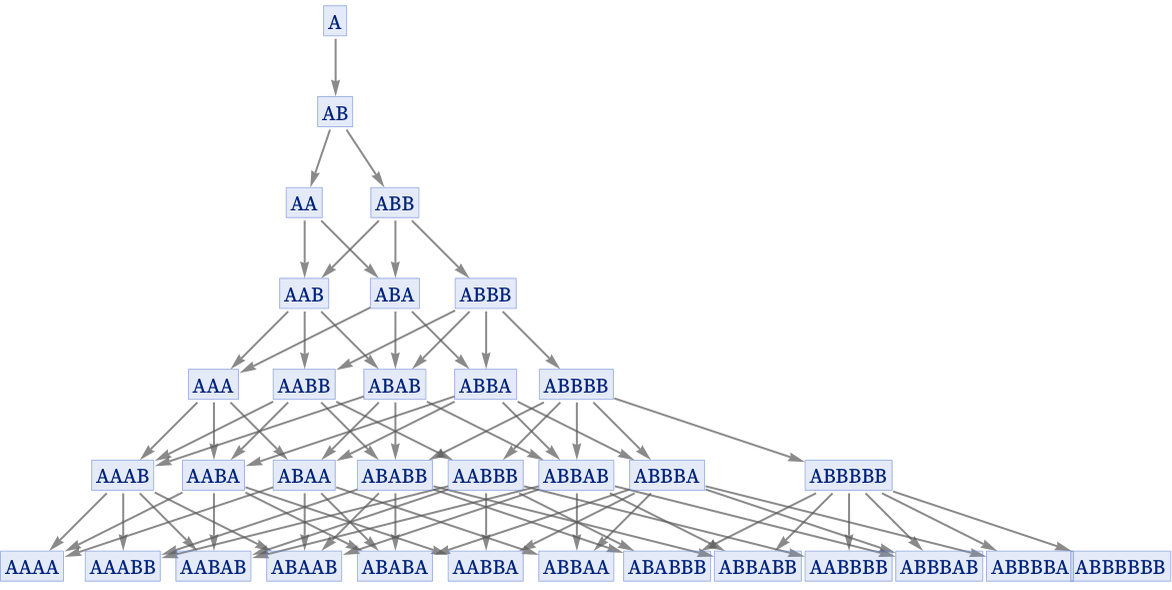
We will discuss this in more detail below. But the basic idea is as follows. Imagine that our universe is based on a simple string substitution system such as {A  AB}. If we start from a state AA, as in the picture above, the multiway evolution from this state immediately leads to multiple outcomes, associated with different updating events. But let us say that we just wanted some kind of “classical” summary of the evolution, ignoring all these different branches.

One thing we might do is not trace individual updates, but instead just look at “generational states” (5.21) in which all updates that can consistently be applied together have been applied. And with the particular rule shown here, we then get the unique sequence of states highlighted above. And as we will discuss below, we can indeed consider these generational states as corresponding to definite (“classical-like”) states of the system, that can consistently be thought of as potential results of measurements.

But now let us imagine how this might work in something closer to a complete experiment. We are running the multiway system shown above. Multiple states are being generated. But at some moment we as observers notice that actually several states that have been produced (say ABBA and AABB) can be combined together to form a consistent generational state (ABBABB). But even though these states ultimately had a common ancestor, they now seem to be on different “branches of history”.

But now causal invariance makes a crucial contribution. Because it implies that all such different branches must eventually converge. And indeed after a couple of steps, the fully assembled generational state ABBABB appears in the multiway system. To us as observers this is in a sense the state we were looking for (it is the “result of our measurement”), and as far as possible, we want to use it as our description of the system.

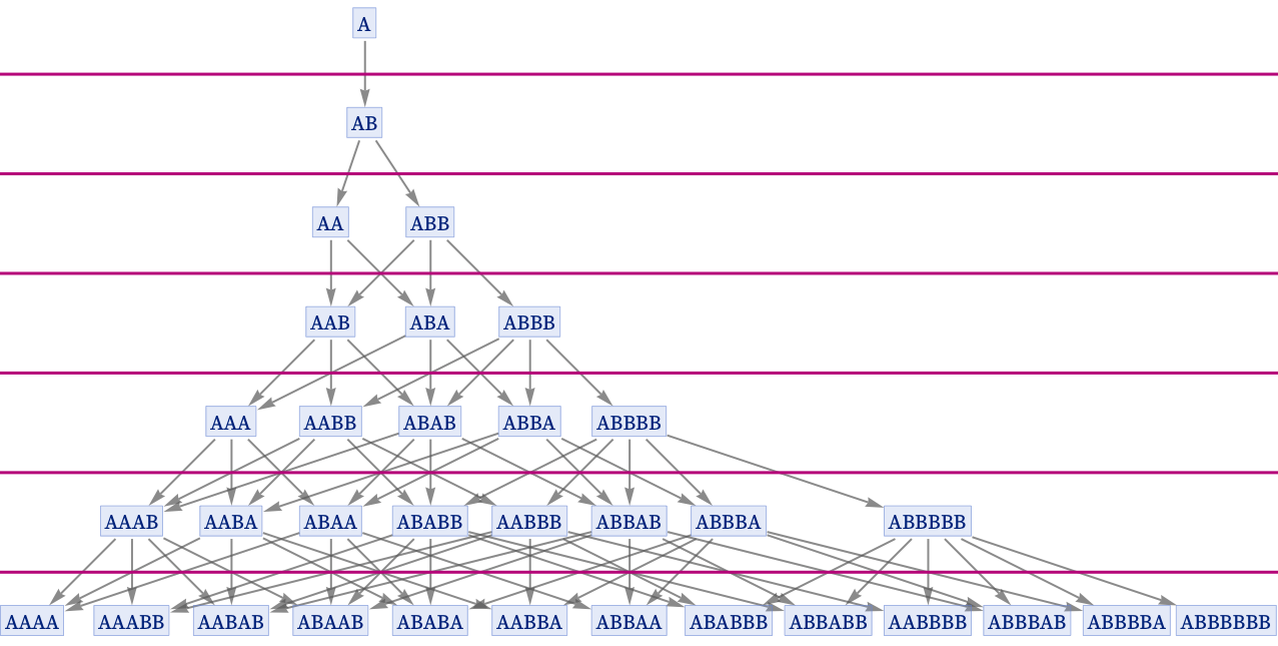
And by setting up an appropriate quantum observation frame, that is exactly what we can do. For example, as illustrated in the picture above, we can make the foliation we choose effectively freeze the generational state, so that in the description we use of the system, the state stays the same in successive slices.

The structure of the multiway system puts constraints on what foliations we can consistently set up. In the case shown here, it does allow us to freeze this particular state forever, but to do this consistently, it effectively forces us to freeze more and more states over time. And as we will see later, this kind of spreading of effects in the multiway graph is closely related to decoherence in the standard formalism of quantum mechanics.

In what we just discussed, causal invariance is what guarantees that states the observer notices can consistently be assembled to form a generational (“classical-like”) state that will always actually converge in the multiway system to form that state. But it is worth pointing out that (as discussed in [121]) strict causal invariance is not ultimately needed for a picture like this to work.

Recall that the observer themselves is also a multiway system. So “within their consciousness” there will usually be many “simultaneous” states. Looked at formally from the outside, the observer can be seen to involve many distinct states. But one could imagine that the internal experience of the observer would be in effect to conflate these states.

Causal invariance ensures that branches in the multiway system will actually merge—just as a result of the evolution of the multiway system. But if the observer “experientially” conflates states, this in effect represents an additional way in which different branches in the multiway system will at least appear to merge [121]. Formally, one can think of this—in analogy to the operation of automated theorem-proving systems—as like the observer “adding lemmas” that assert the equivalence of branches, thereby allowing the system to be “completed” to the point where relevant branches converge. (For a given system, there is still the question of whether only a sufficiently bounded number of lemmas is needed to achieve the convergence one wants.)

Independent of whether there is strict causal invariance or not, there is also the question of what kinds of quantum observation frames are possible. In the end—just like in the spacetime case—such frames reflect the description one is choosing to make of the world. And setting up different “coordinates”, one is effectively changing one’s description, and picking out different aspects of a system. And ultimately the restrictions on frames are computational ones. Something like an inertial frame in spacetime is simple to describe, and its coordinates are simple to compute. But a frame that tries to pick out some very particular aspect of a quantum system may run into issues of computational irreducibility. And as a result, much as happens in connection with the Second Law of thermodynamics [1:9.3], there can still for example be elaborate correlations that exist between different parts of a quantum system, but no realistic measurement—defined by a computationally feasible quantum observation frame—will succeed in picking them out.