8.11 Cosmology, Expansion & Singularities

In our models the evolving hypergraph represents the whole universe, and the expansion of the universe is potentially a consequence of the growth of the hypergraph. In the minimal case of a model involving a single transformation rule, the growth of the hypergraph must be monotonic, although the rate can vary depending on the local structure of the hypergraph. If there are multiple transformation rules, there can be both increase and decrease in hypergraph size. (Even with a single rule, there is also still the possibility—discussed below—of effective size decrease as a result of pieces of the hypergraph becoming disconnected.)

In the case of uniform growth, measurable quantities such as length and energy would essentially all continually scale as the universe evolves. The core structure of particles—embodied for example in topological-like features of the hypergraph—could potentially persist even as the number of nodes “within them” increases. Since the rate of increase in size in the hypergraph would undoubtedly greatly exceed the measurable growth rate of the universe, uniform growth implies a kind of progressive refinement in which the length scale of the discrete structure of the hypergraph becomes ever more distant from any given measured length scale—so that in effect the universe is becoming an ever closer approximation to continuous.

In traditional cosmology, one thinks of the universe as effectively having exactly three dimensions of space (cf. [120]). In our models, dimension is in effect a dynamical variable. Possibly some of what is normally attributed to curvature in space can instead be reformulated as dimension change. But even beyond this, there is the potential for new phenomena associated, for example, with local change of dimension. In general, a change of dimension—like curvature—affects the density of geodesics. Changes of dimension generated by an underlying rule may potentially lead to effects that for example mimic the presence of mass, or positive or negative energy density. (There could also be dimension-change “waves”, perhaps with some rather unusual features.)

In our models, the universe starts from some initial configuration. It could be something like a single self-loop hypergraph. Or in the multiway system it could be multiple initial hypergraphs. (Note that we can always “put the initial conditions into the rule” by adding a rule that says “from nothing, create the initial conditions”.)

An obvious question is whether any traces of the initial conditions might persist, perhaps even through the whole evolution of the system. The effective randomness associated with computational irreducibility in the evolution will inevitably tend to “encrypt” most features of the initial conditions [1:9.3] to the point where they are unrecognizable. But it is still conceivable that, for example, some global symmetry breaking associated with the first few hypergraph updating events could survive—and the remote possibility exists that this could be visible today in the large-scale structure of the universe, say as a pattern of density fluctuations in the cosmic microwave background.

Our models have potentially important implications for the early universe. If, for example, the effective dimension of the universe was initially much higher than 3 (as is basically inevitable if the initial conditions are small), there will have been a much higher level of causal contact between different parts of the universe than we have deduced by extrapolating the 3D expansion of the universe today [1:p1055]. (In effect this happens because the volume of the past light cone will grow like t^d—or perhaps exponentially with t—and not just like t³.)

As we discussed in 2.9, it is perfectly possible in our models for parts of the hypergraph to become disconnected as a result of the operation of the rule. But assuming that the rule is local (in the sense that its left-hand side is a connected hypergraph), pieces of the hypergraph that become disconnected can never interact again. Even independent of outright disconnection of the spatial graph, it is also possible for the causal graph to “tear” into disconnected parts that can never interact again (see 6.10):

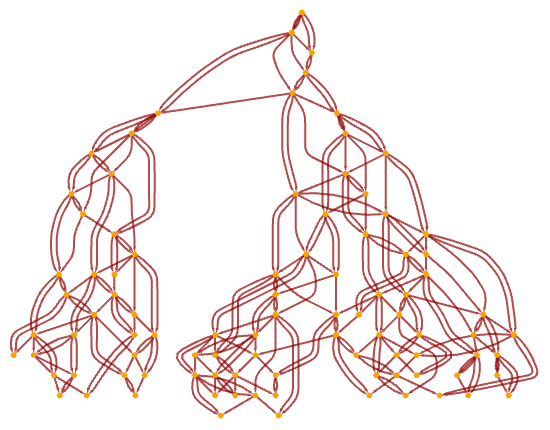
A disconnection in the causal graph corresponds to an event horizon in our system—that cannot be crossed by any timelike curve. (And indeed our causal graphs—consisting as they do of “elementary light cones knitted together”—are like microscopic analogs of the causal diagrams often used in studying general relativity. Note that in our models, as in ordinary general relativity, there are two kinds of event horizons: “cosmic”—like the one above—in which effectively two distinct subuniverses are created, and “black hole”, in which there is a region of the causal graph with incoming, but not outgoing, edges.)

We can also ask about other extreme phenomena in spacetime. Closed timelike curves correspond to loops in the causal graph, and with some rules they can occur. But they do not represent any real form of “time travel”; they just correspond to the presence of states that are precisely repeated as a result of the evolution of the system. (Note that in our models, time effectively corresponds to the progression of computation, and has a very different underlying character from something like space.)

Wormholes and effective faster-than-light travel are not specifically excluded by the structure of our models, especially insofar as there can potentially be deviations in the effective local dimensionality of space. But insofar as the conditions to get general relativity as a limiting effective theory are satisfied, these will occur only in the circumstances where they do in that theory.