3.5 Rules Depending on a Single Binary Relation

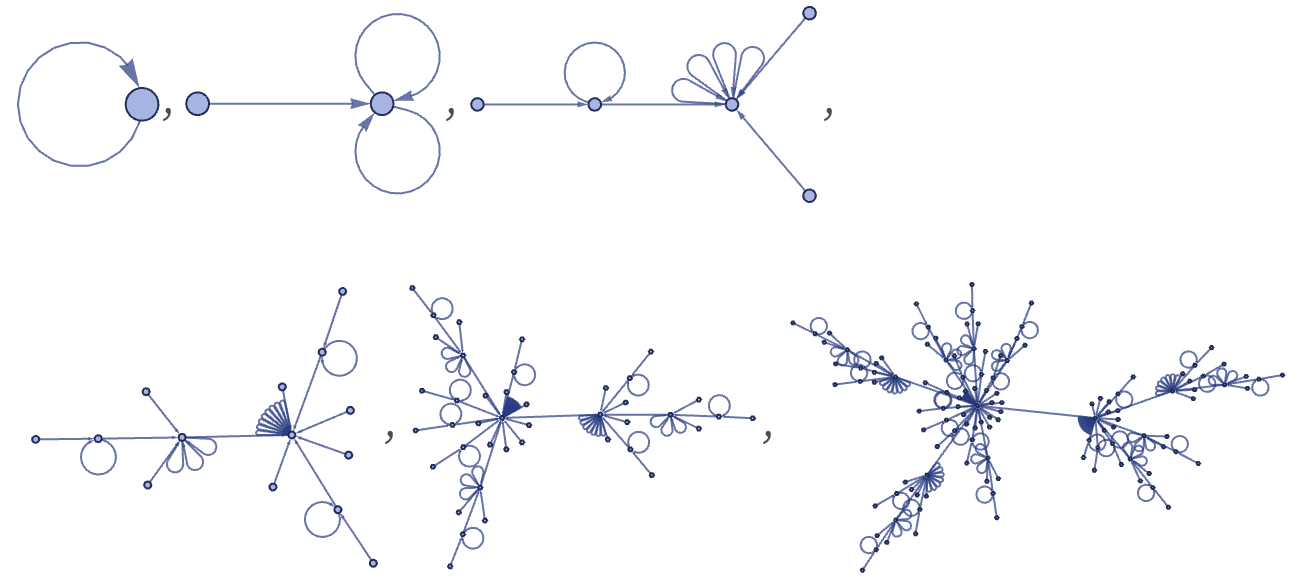
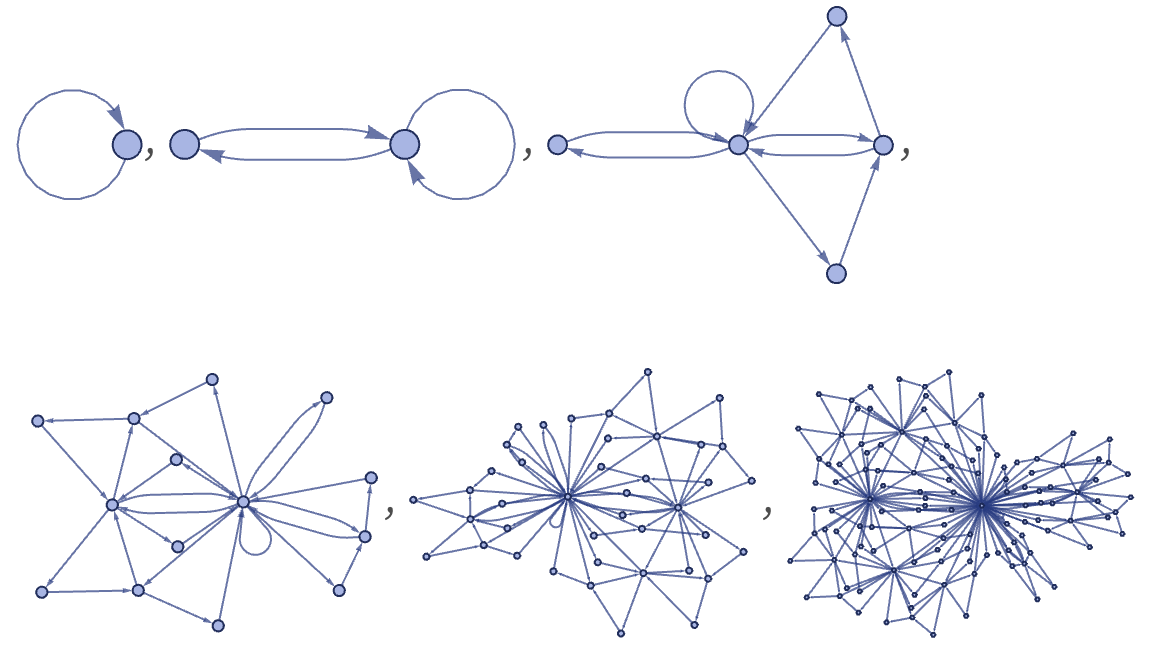
There are 73 inequivalent left-connected 1₂  2₂ rules, but none lead to structures more complex than trees. Starting each from a single self-loop, the results after 5 steps are (note that even a connected rule like {{x,y}}→{{x,z},{z,x}} can give a disconnected result):

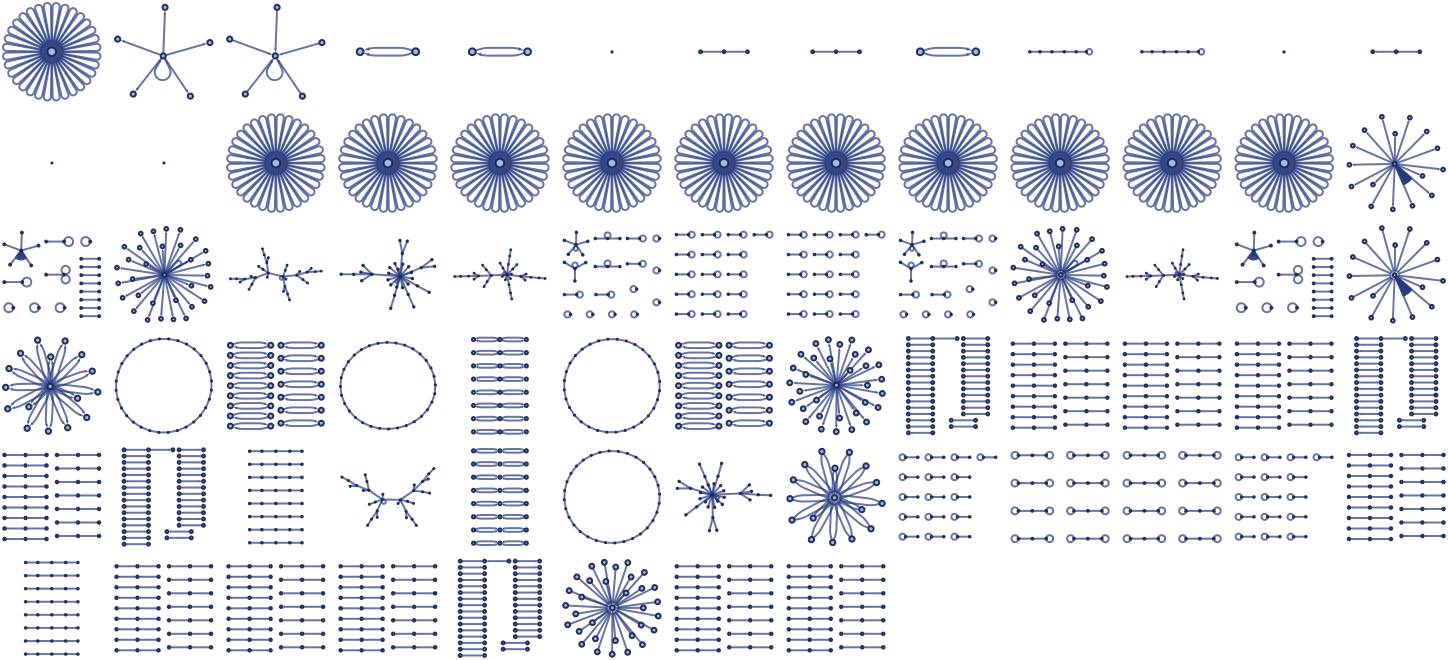
With an initial condition consisting of a square graph, the following very similar results are obtained:

There are 506 inequivalent left-connected 1₂  3₂ rules. Running all these rules for 5 steps starting from a single self-loop, and keeping only distinct connected results, one gets (note that similar-looking results can differ in small-scale details):

Several distinct classes of behavior are visible. Beyond simple lines, loops, trees and radial “bursts”, there are nested (“cactus-like”) graphs such as

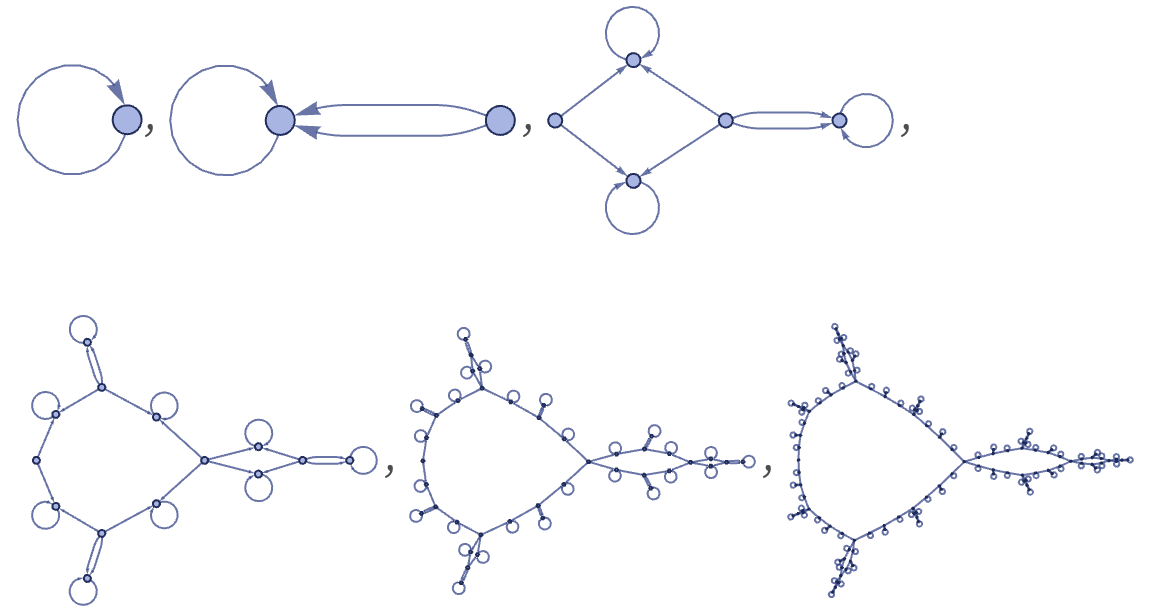
obtained from the rule:

The only slightly different rule

gives a rather different structure:

A layered rendering makes the behavior slightly clearer:

Another notable rule similar to one we saw in the previous section is:

From a single edge this gives:

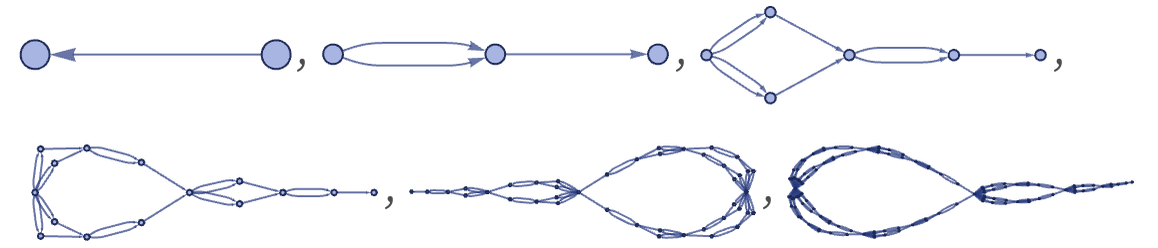
Starting from a single self-loop gives a more complex topological structure (and copies of this structure appear when the initial condition is more complex):

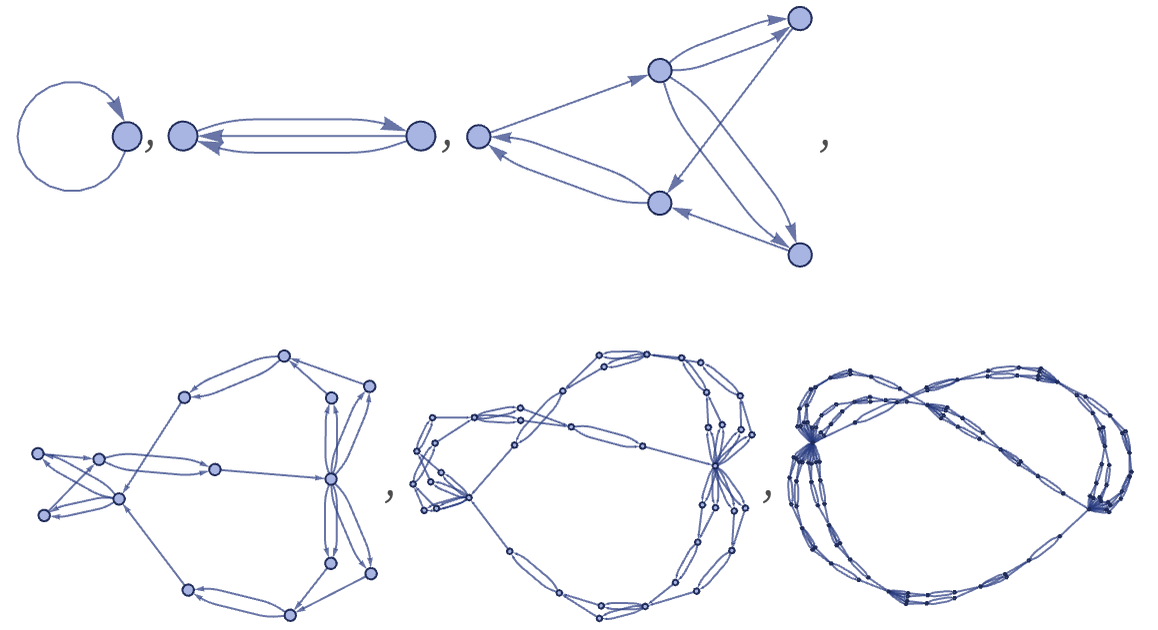
Another notable 1₂  2₂ rule is

which produces an elaborately filled-in structure:

After 8 steps, the structure has the form:

After t steps, there are 3^t–1 nodes, and edges. The graph diameter is 2t – 1 if directions of edges are taken into account, and t – 1 if they are not. The maximum degree of any vertex is 2^t—and all vertices have degrees of the form 2^s, with the number of vertices of degree 2^s being proportional to 3^t–s.

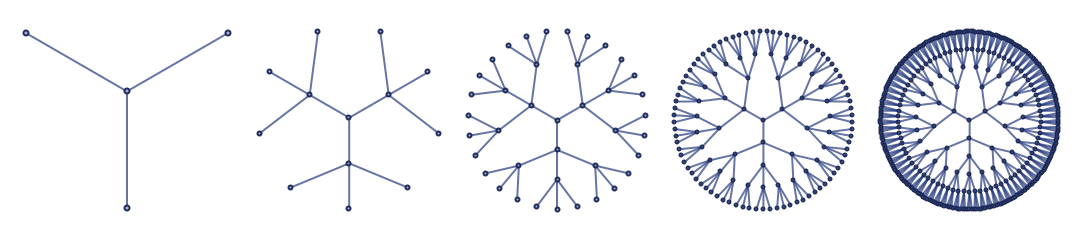
Starting from a single edge makes it slightly easier to understand what is going on:

As the rule indicates, every edge of every triangle “sprouts” a new triangle at every step, in effect producing a sequence of “frills upon frills”. But even though this may seem complicated, the whole structure basically corresponds just to a ternary tree in which each node is replaced by a triangle:

Starting from a single self-loop, all 1₂  3₂ rules give after n steps a number of relations that is either constant, or goes like 2t – 1, 2^t – 1 or 3^t–1.

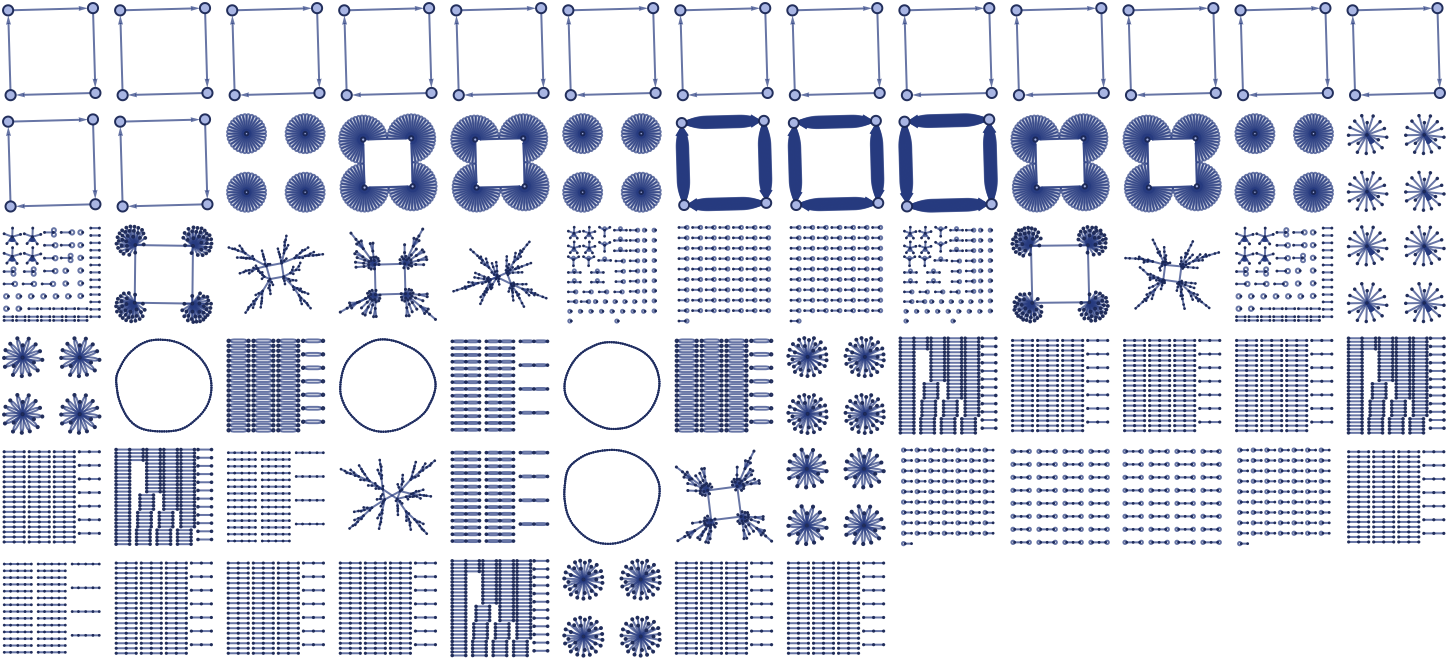
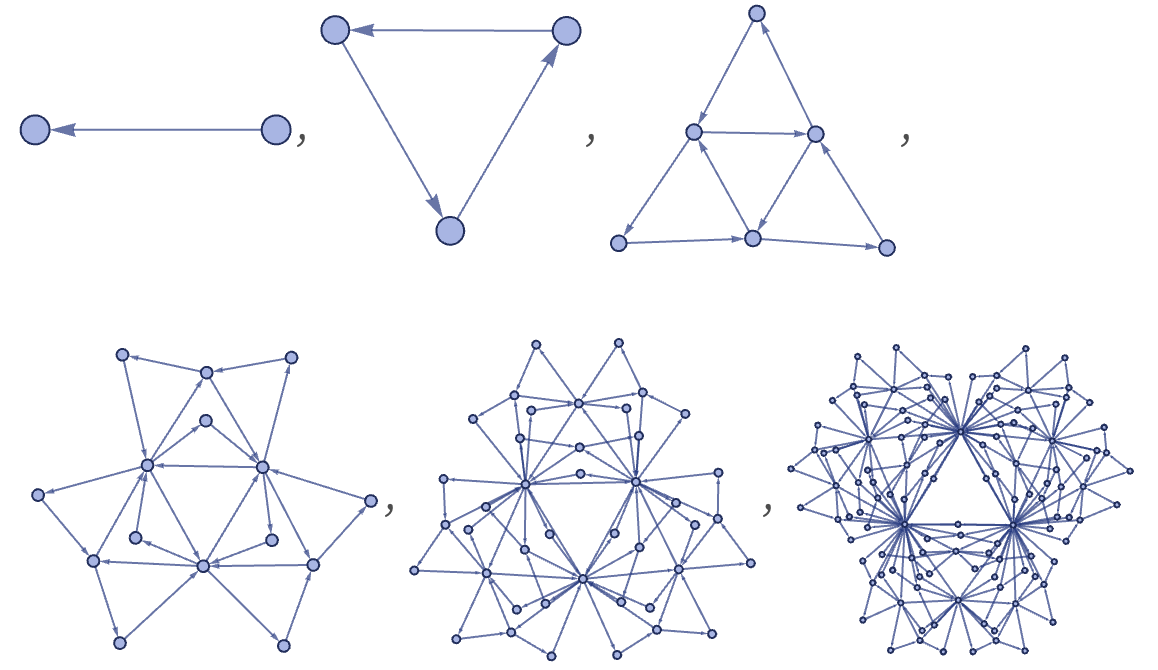
For 1₂  4₂, there are 3740 distinct left-connected rules. As suggested by the random cases below, their behavior is typically similar to 1₂  3₂ rules, though the forms obtained can be somewhat more elaborate:

For example, the rule

gives the following:

The rule

gives a nested form:

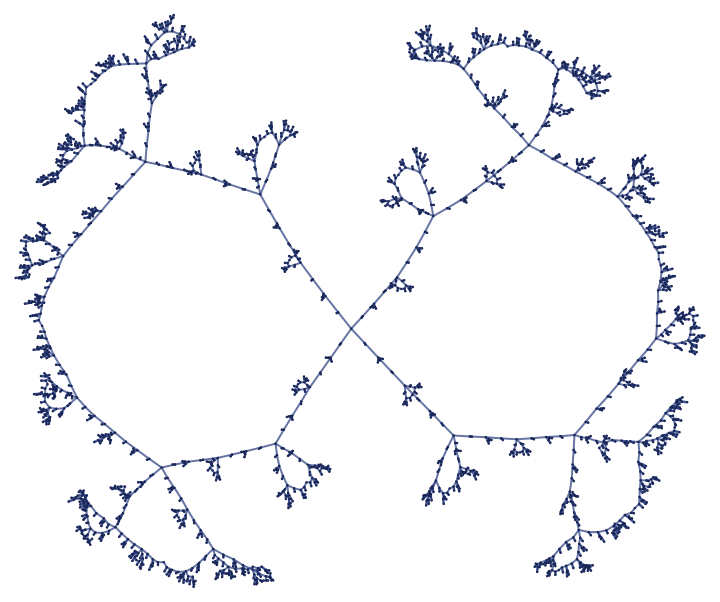
The rule

gives

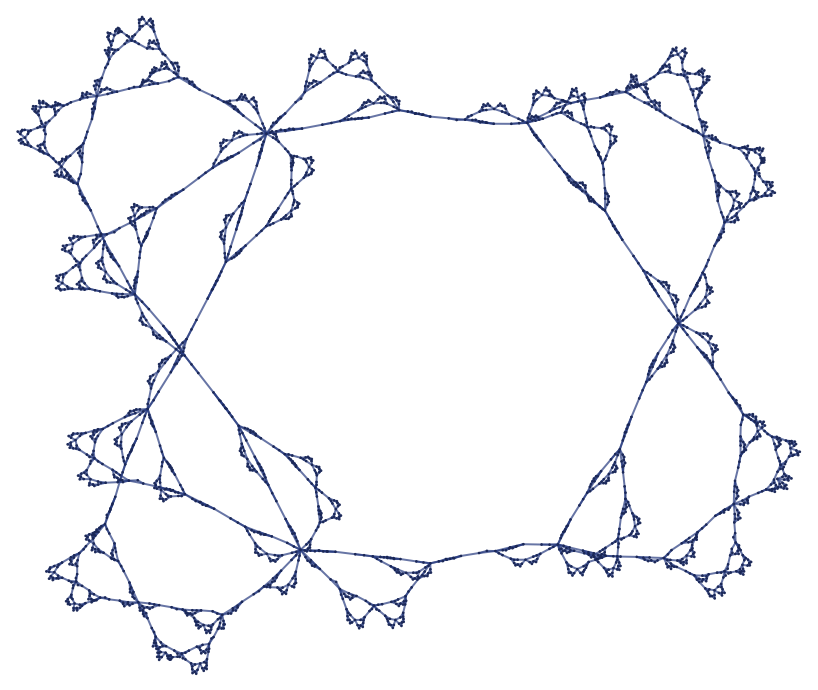
while the similar rule

gives:

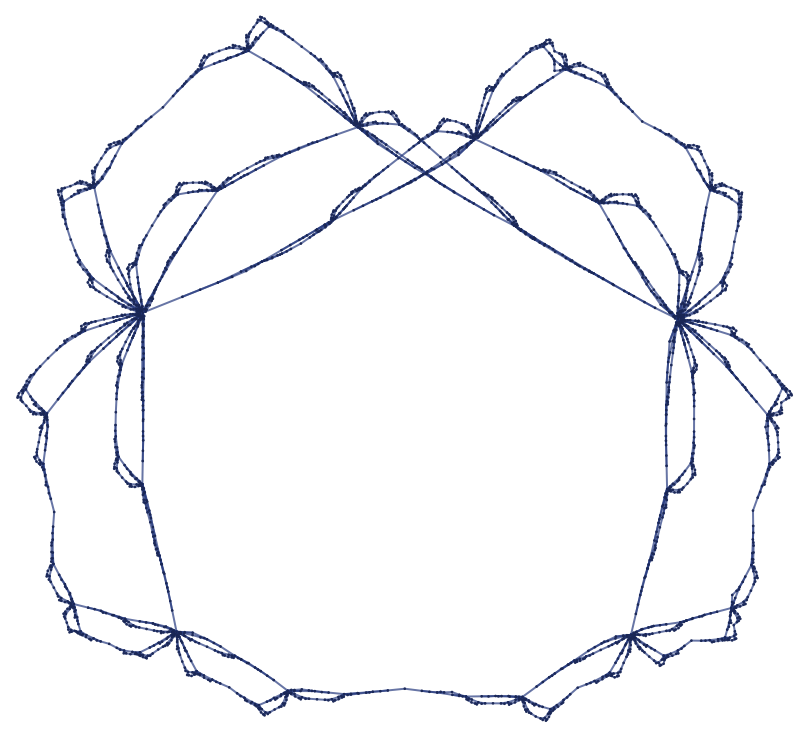
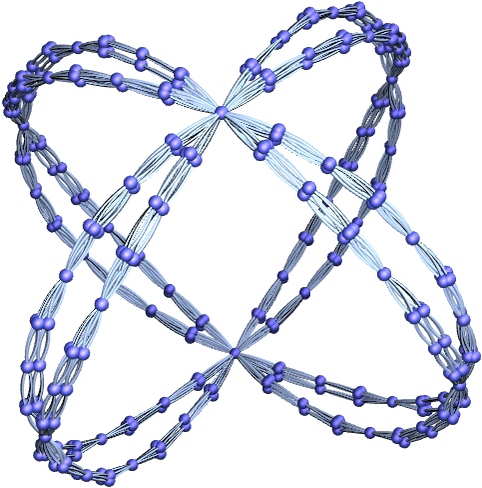
Successive steps in effect just fill in this shape, which seems somewhat irregular when rendered in 2D, but appears more regular if rendered in 3D.

Another rule with a simple structure when rendered in 3D is

which yields:

The outputs from 1₂  4₂ rules all grow either linearly (for example, like 3t – 2), or exponentially, asymptotically like 2^t, 3^t or 4^t. The number of relations after t steps is always given by a linear recurrence relation; for the rule {{x,x}}{{x,x},{x,x},{x,y},{x,y}} the recurrence is f[t]=3f[t–1]–2f[t–2] (with f[1]=1, f[2]=4), giving size .