3.6 Rules Depending on One Ternary Relation

There are 9373 inequivalent left-connected 1₃  2₃ rules. Here are typical examples of their behavior after 5 steps, starting from a single ternary self-loop:

Here are results from a few of these rules after 10 steps:

The number of relations in the evolution of 1₃  2₃ rules can grow in a slightly more complicated way than for 1₂  n₂ rules. In addition to linear and 2^t growth, there is also, for example, quadratic growth: in the rule

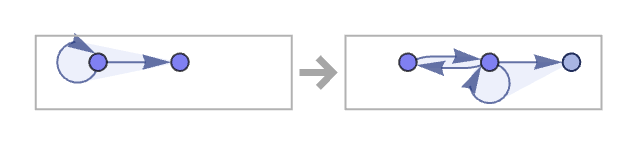
each existing “arm” effectively grows by one element each step, and there is one new arm generated, yielding a total size of

= :

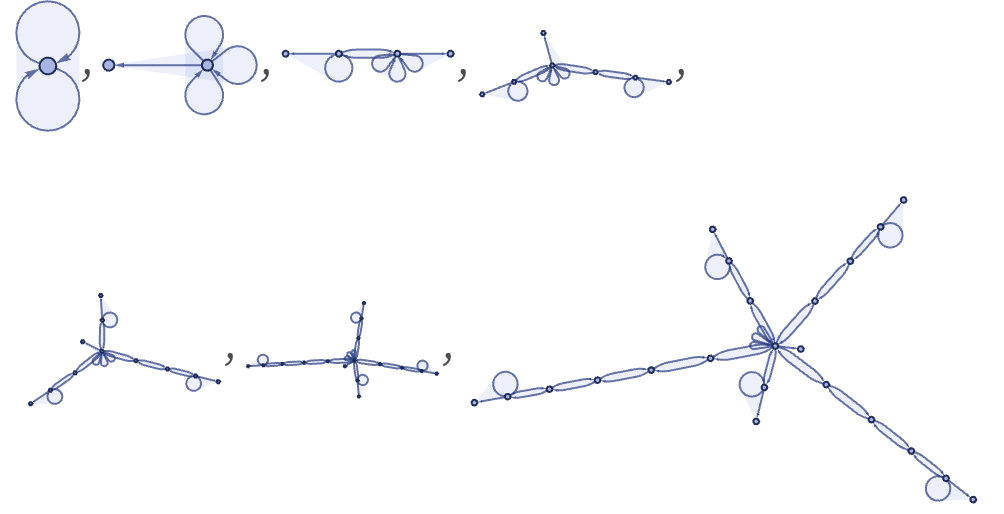
The rule

yields a Fibonacci tree, with size Fibonacci[t+2]–1 ∼ :

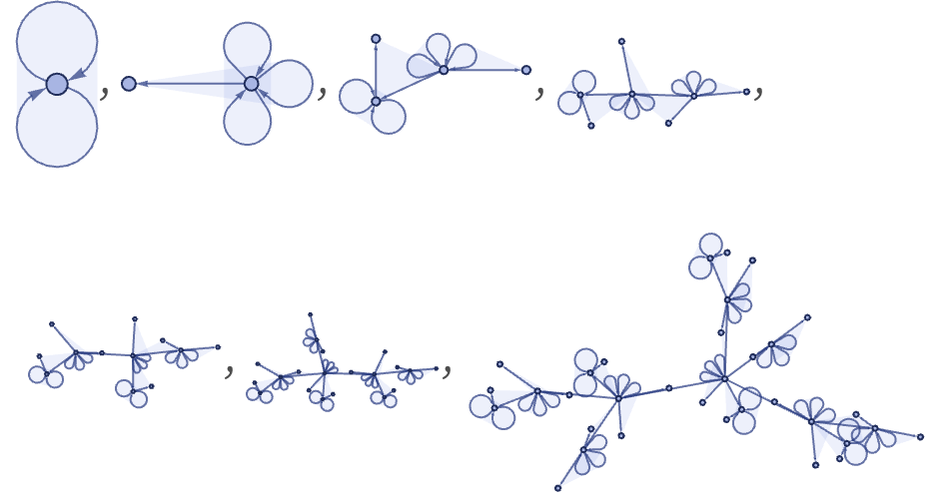
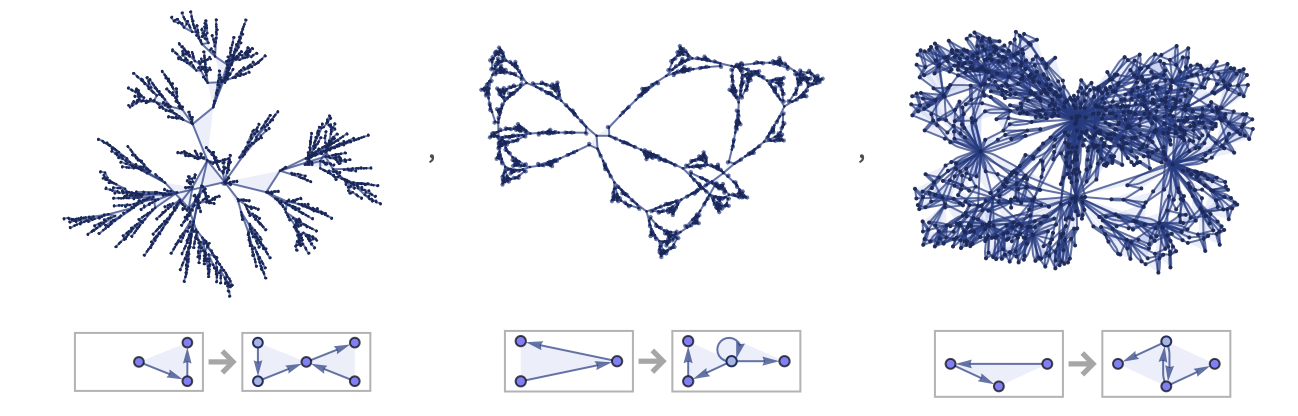
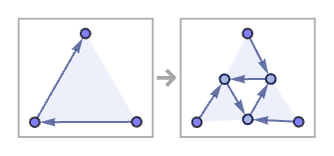
1₃  2₃ rules can produce results that look fairly complex. But it is a consequence of their dependence only on a single relation that once such rules have established a large-scale structure, later updates (which are necessarily purely local) can in a sense only embellish it, not fundamentally change it:

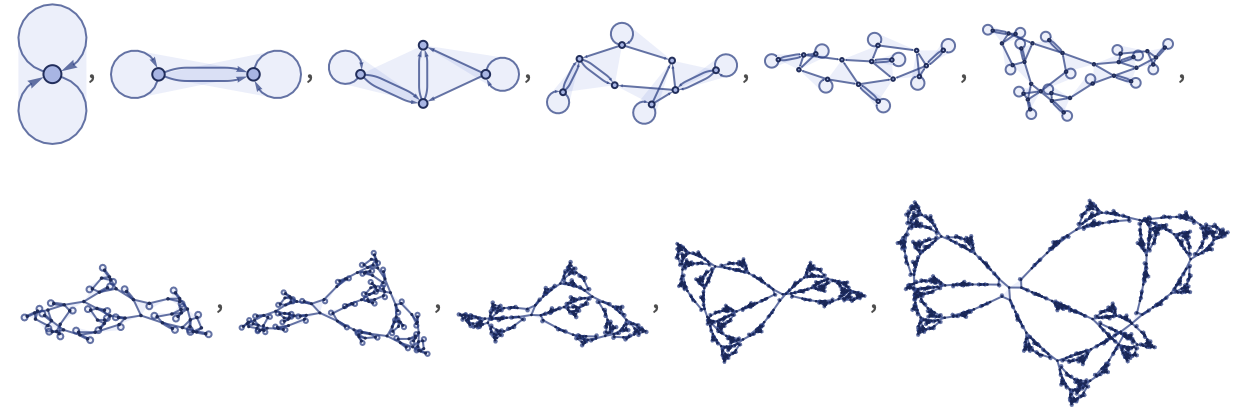
There are 637,568 inequivalent left-connected 1₃  3₃ rules; here are samples of their behavior:

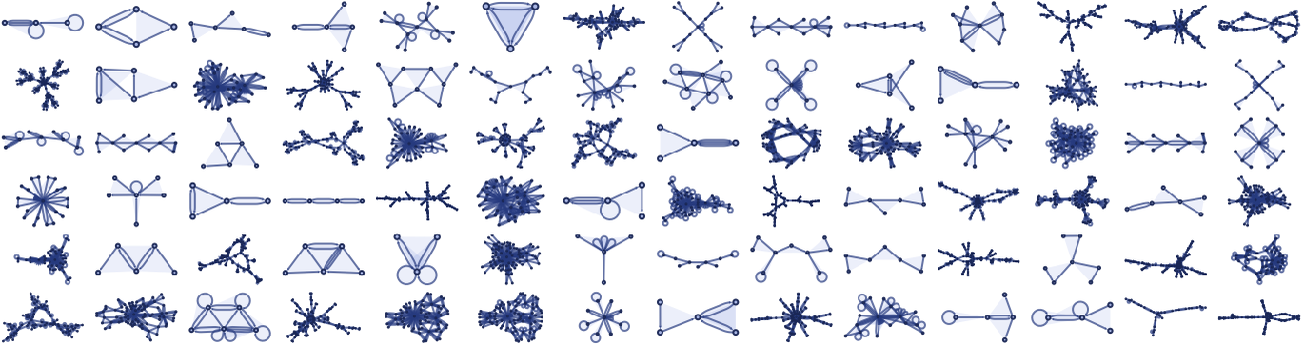
The results can be more elaborate than for 1₃  2₃ rules—as the following examples illustrate—but remain qualitatively similar:

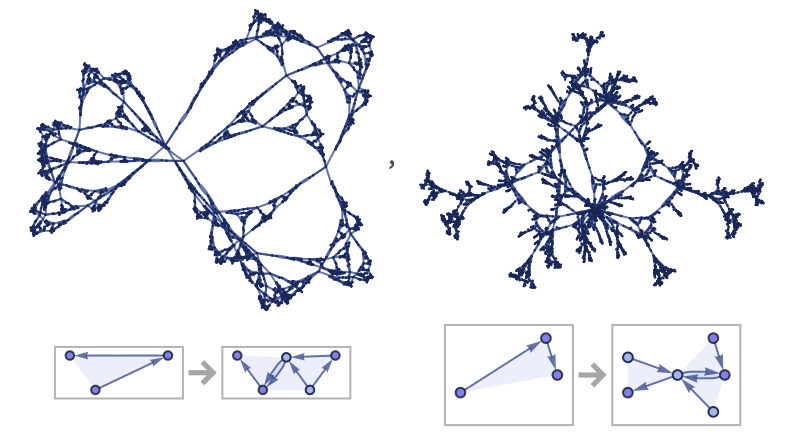
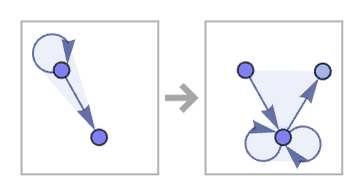
One notable 1₃  3₃ rule (that we will discuss below) in a sense directly implements the recursive formation of a nested Sierpiński pattern: