A Class of Models with the Potential to Represent Fundamental Physics
  1. Introduction
  2. Basic Form of Models
  3. Typical Behaviors
  4. Limiting Behavior and Emergent Geometry
  5. The Updating Process for String Substitution Systems
  6. The Updating Process in Our Models
  7. Equivalence and Computation in Our Models
  8. Potential Relation to Physics
  9. Additional Material
  10. References
  11. Index
Download PDf download pdf
ARXIV ARXIV
peer-review peer review
technical introduction Limiting Behavior and Emergent Geometry

4.2 Hyperbolic Space

Among all possible rules, the formation of geometrical shapes of the kind we have just been discussing is very rare. Slightly more common is the type of behavior that we see in a rule like:

{{x, y}, {y, z}} -> {{w, x}, {w, y}, {x, y}, {y, z}}
RulePlot[ResourceFunction[ "WolframModel"][{{x, y}, {y, z}} -> {{w, x}, {w, y}, {x, y}, {y, z}}]]
Graph[Rule @@@ #, GraphLayout -> "SpringElectricalEmbedding", ImageSize -> Tiny, VertexStyle -> ResourceFunction["WolframPhysicsProjectStyleData"]["SpatialGraph", "VertexStyle"], EdgeStyle -> ResourceFunction["WolframPhysicsProjectStyleData"]["SpatialGraph", "EdgeLineStyle"]] & /@ ResourceFunction[ "WolframModel"][{{x, y}, {y, z}} -> {{w, x}, {w, y}, {x, y}, {y, z}}, {{0, 0}, {0, 0}}, 9, "StatesList"]

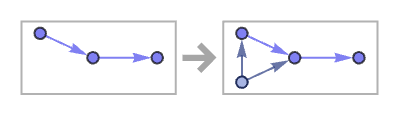
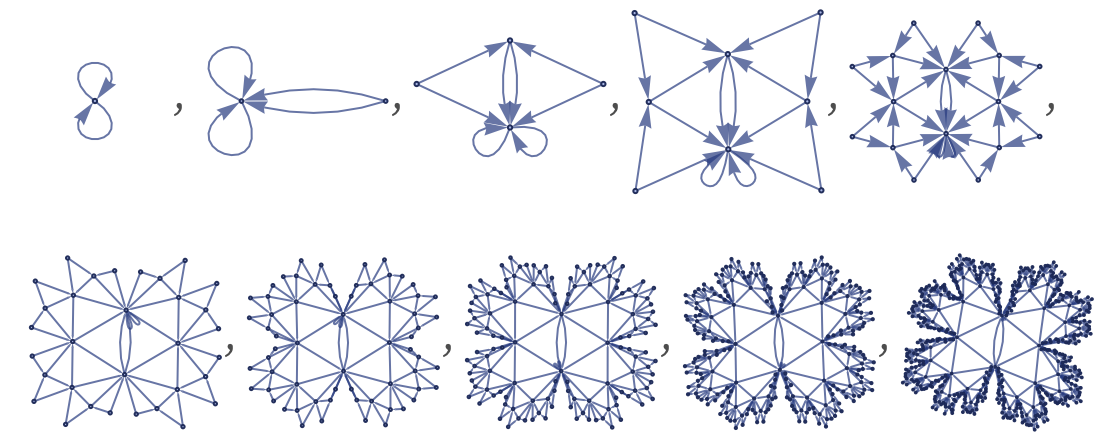
Essentially the same behavior also occurs in a mixed-arity rule with a single relation on the left-hand side:

{{x, y}} -> {{z, y, x}, {y, z}, {z, x}}
RulePlot[ResourceFunction[ "WolframModel"][{{x, y}} -> {{z, y, x}, {y, z}, {z, x}}]]
Flatten[Append[ ResourceFunction["WolframModelPlot"][#, "MaxImageSize" -> 100] & /@ ResourceFunction[ "WolframModel"][{{x, y}} -> {{z, y, x}, {y, z}, {z, x}}, {{0, 0}}, 7, "StatesList"], {ResourceFunction["WolframModelPlot"][ ResourceFunction[ "WolframModel"][{{x, y}} -> {{z, y, x}, {y, z}, {z, x}}, {{0, 0}}, 8, "FinalState"], "MaxImageSize" -> 100, VertexCoordinateRules -> { 1 -> {10.17470974389601, 8.49613742700209}, 3 -> {5.522696341420668, 7.338440718767156}, 6 -> {6.3409702377458155`, 4.311759255597379}, 7 -> {5.496888459165139, 10.472976361208069`}, 12 -> {3.615129292794065, 4.450896697724719}, 13 -> {8.4834898391255, 3.766154816205485}, 14 -> {7.394559375500452, 11.633466188026262`}, 15 -> {2.8984489031323792`, 9.605475891687881}, 24 -> {3.895172802770809, 2.840468525286524}, 25 -> {2.985887559656875, 5.67951058539453}, 26 -> {9.705650118588965, 4.6138773593047375`}, 27 -> {6.971951283425833, 2.168266710532894}, 28 -> {5.483577197699321, 12.73655210751767}, 29 -> {8.7719756599412, 11.234319688281573`}, 30 -> {2.6065366385527637`, 8.230190879914598}, 31 -> {2.7362421862854522`, 11.234118436779987`}, 48 -> {2.6104867160506307`, 2.770610986610823}, 49 -> {4.743472706572571, 2.6262659671477575`}, 50 -> {3.540819922379263, 6.463609329320128}, 51 -> {1.9400317339712698`, 4.5219696852351845`}, 52 -> {9.359034857699994, 2.9573980903550328`}, 53 -> {9.7744564327544, 5.7134912930396275`}, 54 -> {6.054569140344993, 2.2329413652144137`}, 55 -> {7.810359332633349, 1.7201595953950017`}, 56 -> {6.157928916138276, 13.43101395008935}, 57 -> {4.63310743523114, 12.40996821196174}, 58 -> {9.292251306406886, 10.29264323347189}, 59 -> {7.975647412991421, 12.786275585073462`}, 60 -> {1.298412074095909, 9.080242385549548}, 61 -> {3.3459073735497626`, 7.591555166611972}, 62 -> {3.4989145850458265`, 11.642225441828133`}, 63 -> {1.4776734738176203`, 10.967150300145452`}, 96 -> {2.6265786460091918`, 1.9877656342767989`}, 97 -> {2.3999069988493984`, 3.2813803053477923`}, 98 -> {5.249912896997562, 3.1018501323600587`}, 99 -> {3.7828523421324425`, 1.8184148918204628`}, 100 -> {2.3236435514081957`, 5.985684236440766}, 101 -> {4.226436985543674, 6.845361219968333}, 102 -> {2.0760875908713823`, 3.9765707592100723`}, 103 -> {1.527821895377047, 4.9860118385133925`}, 104 -> {9.84876882196794, 3.159437438000381}, 105 -> {8.870775373288968, 2.4930122847313956`}, 106 -> {9.713215771465247, 6.4273452299596885`}, 107 -> {9.564443374464055, 4.695650922862196}, 108 -> {6.189775047562619, 1.2005698384463175`}, 109 -> {5.870942968708712, 2.856650647566711}, 110 -> {8.203304931214394, 2.1457231834793618`}, 111 -> {7.235115999016531, 0.9031052519385188}, 112 -> {5.341861835395375, 14.01802403630179}, 113 -> {6.676217641866845, 13.150808370635533`}, 114 -> {4.639102506185069, 11.759231589519993`}, 115 -> {4.46964750087078, 13.450833824145157`}, 116 -> {9.016294317888168, 11.491306163738942`}, 117 -> {9.324712327813536, 9.483695256436661}, 118 -> {7.387402164569019, 13.041722819752499`}, 119 -> {8.480836067034538, 12.790499516136181`}, 120 -> {1.0175063412620267`, 8.517774213006785}, 121 -> {1.2842755208751715`, 9.648945645876593}, 122 -> {4.106322307324142, 7.622664064007106}, 123 -> {2.041436015749269, 7.71235477691487}, 124 -> {2.360864094882011, 12.182473720501463`}, 125 -> {4.136196607784628, 11.344981944377079`}, 126 -> {1.4160857670602205`, 10.415930600982302`}, 127 -> {1.2835747076180641`, 11.725459301967838`}, 192 -> {2.0605343341705344`, 1.855543156917466}, 193 -> {2.951337055647875, 1.9326988633882491`}, 194 -> {2.6503322363490667`, 3.634247736365396}, 195 -> {1.8831410865730231`, 2.592977474834938}, 196 -> {4.7117874795572, 2.258614373212065}, 197 -> {5.507986998304639, 3.5727581484903213`}, 198 -> {3.3928863219780556`, 1.7956816594501495`}, 199 -> {4.030541053506976, 1.5965062639952539`}, 200 -> {2.4126927621381484`, 6.239169757610148}, 201 -> {1.993384811031858, 5.6902173679425525`}, 202 -> {4.663096900739548, 6.990433952542747}, 203 -> {3.3935442478727955`, 6.565465859574131}, 204 -> {1.324961996319851, 3.9187174952680772`}, 205 -> {2.4714018034136513`, 3.964098169729651}, 206 -> {1.7583015325366371`, 5.256304300292178}, 207 -> {1.0023278842983847`, 4.530770171567826}, 208 -> {9.786668835484088, 2.432248416002552}, 209 -> {9.948506215284393, 3.5282724205299636`}, 210 -> {8.56337519631959, 2.703035079087936}, 211 -> {9.195870791017624, 2.043545277484997}, 212 -> {9.453227824296258, 5.862678627849127}, 213 -> {9.760124390150489, 6.818075025592382}, 214 -> {9.530018631915722, 4.168840988006668}, 215 -> {9.467628925052926, 4.9701284089048015`}, 216 -> {5.798428706239622, 1.0842086338706933`}, 217 -> {6.482929233335493, 1.052079096074601}, 218 -> {5.907983446844438, 3.347020887766741}, 219 -> {5.66721804704877, 1.9770175999694504`}, 220 -> {8.036121999275705, 1.2383188948813042`}, 221 -> {8.206638817742807, 2.613926297780714}, 222 -> {6.913404064236986, 0.9420147932776375}, 223 -> {7.533885422605626, 0.5855590352420348}, 224 -> {5.53534194758248, 14.41945841669519}, 225 -> {5.043689800326046, 13.89330569355554}, 226 -> {6.813267843508938, 12.697925406148947`}, 227 -> {6.269316939980895, 13.989899808151852`}, 228 -> {4.205252245004947, 12.555596907314735`}, 229 -> {4.8038092945374515`, 11.302690474098675`}, 230 -> {4.720908934682256, 13.678544129069051`}, 231 -> {4.0629689798184, 13.450733774753438`}, 232 -> {9.14889398710512, 11.239376726671393`}, 233 -> {8.731406979969686, 11.931213888824908`}, 234 -> {9.42538430770116, 8.98925299915938}, 235 -> {8.93212552219056, 10.112468313284895`}, 236 -> {7.574149461906626, 13.618221989401357`}, 237 -> {7.168391526666329, 12.720759256428687`}, 238 -> {8.59323574079489, 12.437982496182078`}, 239 -> {8.2248800916467, 13.506578453642224`}, 240 -> {0.3954149682270211, 8.820653643679009}, 241 -> {1.3020785200396694`, 8.30520045815128}, 242 -> {1.6621713724958307`, 9.766291503487286}, 243 -> {0.5434946366412812, 9.510233170570245}, 244 -> {3.215283797799815, 7.743105658801523}, 245 -> {4.617948919083308, 7.612715441795215}, 246 -> {1.6465575462112751`, 7.914964805554587}, 247 -> {2.1983844797056356`, 7.475321580418564}, 248 -> {2.549407325777497, 12.451426854459541`}, 249 -> {1.9759388269268425`, 12.108507647160456`}, 250 -> {4.506638457006838, 10.97099084325866}, 251 -> {3.3193991054790533`, 11.896335192925319`}, 252 -> {0.7309589207606464, 10.943348448769393`}, 253 -> {1.7476992060481733`, 10.13382023278189}, 254 -> {1.5808897877956716`, 11.865005944651491`}, 255 -> {0.7001102298755331, 11.707638271311527`}, 256 -> {18.7387554885444, 1.2794820788594188`}, 257 -> {18.35944764914279, 1.5153297101981624`}, 258 -> {18.1875670272798, 2.9271234608181245`}, 259 -> {18.95542130386331, 1.9546039496195315`}, 260 -> {17.77052414654499, 2.1687257867118612`}, 261 -> {17.12593520460679, 3.3327645987765284`}, 262 -> {18.43645318704022, 1.779902210261322}, 263 -> {17.989469069153383`, 1.6192032438309973`}, 264 -> {17.33259820889451, 4.298582276697555}, 265 -> {17.89625529395596, 3.9812410552277204`}, 266 -> {15.321927825221675`, 5.006886584367881}, 267 -> {16.458370019541235`, 4.327965533714803}, 268 -> {19.094072030197395`, 2.9932258699664103`}, 269 -> {18.284852453759715`, 3.1299338130061827`}, 270 -> {18.18574910654754, 4.049135442605229}, 271 -> {19.074995841266393`, 3.388018275880864}, 272 -> {15.264242533317995`, 3.4213201492840946`}, 273 -> {15.235103821735498`, 4.477256500634358}, 274 -> {15.933846463544734`, 3.5035360164876947`}, 275 -> {15.466933425514359`, 3.0372004829578576`}, 276 -> {15.897312991700451`, 6.833357088045831}, 277 -> {15.304936289492687`, 7.448722613446059}, 278 -> {15.70919565235456, 5.026894175294209}, 279 -> {15.88735197238305, 6.041477702547438}, 280 -> {17.217420411598578`, 1.496341178371262}, 281 -> {16.765202089269362`, 1.6384124581973951`}, 282 -> {16.892212746029493`, 3.2244525561387083`}, 283 -> {17.29516690078701, 2.044128794703713}, 284 -> {15.97535388084484, 2.1218293085057347`}, 285 -> {15.927415221330929`, 3.316406954035385}, 286 -> {16.54654914376718, 1.6398436559238343`}, 287 -> {16.136292231344925`, 1.60695815838103}, 288 -> {13.082446073904803`, 6.546066190050237}, 289 -> {13.297140307435107`, 6.058367416563898}, 290 -> {11.915836598094568`, 6.792745142797633}, 291 -> {12.510641292578205`, 6.72845138654665}, 292 -> {13.586218302675796`, 5.1840106001373805`}, 293 -> {13.780069887886054`, 6.118003064509507}, 294 -> {13.146065806332398`, 5.574211782157779}, 295 -> {13.188812971106891`, 4.953200167563724}, 296 -> {11.03580978992025, 8.830213270907297}, 297 -> {11.514939294629686`, 8.658904181360896}, 298 -> {9.754976559119925, 8.220436807048149}, 299 -> {10.555214050671585`, 8.359681570361321}, 300 -> {12.625203240946634`, 8.051435222113296}, 301 -> {12.459880745450832`, 7.408725429647387}, 302 -> {11.812348321328578`, 8.517193220724256}, 303 -> {12.424714442563698`, 8.45841413314397}, 304 -> {18.617335853202977`, 5.319590581266202}, 305 -> {18.08324496734576, 5.506321311857555}, 306 -> {17.04882498891599, 6.061441286534572}, 307 -> {18.318274597032758`, 5.673357176255218}, 308 -> {16.79486091600649, 5.42206314312673}, 309 -> {15.54711549559176, 5.307846895296838}, 310 -> {17.961914344911794`, 5.685968517659683}, 311 -> {17.61961673066874, 5.883892173363255}, 312 -> {15.491013509908575`, 6.654111703766665}, 313 -> {16.127015405388743`, 6.3603665778927665`}, 314 -> {14.018570948449465`, 6.636645936233051}, 315 -> {14.84016561137184, 6.741332864172207}, 316 -> {17.471880513979425`, 5.259741053661548}, 317 -> {16.85272216050957, 5.316440582391797}, 318 -> {16.23895649148957, 5.861391787176203}, 319 -> {17.124340469747555`, 5.231500767751133}, 320 -> {14.379410361745288`, 14.65196150826595}, 321 -> {13.809692957063266`, 14.02701574963982}, 322 -> {14.600631607529392`, 13.371663473845777`}, 323 -> {14.718536928888367`, 14.428515916945718`}, 324 -> {13.20935613449849, 12.9627595321291}, 325 -> {13.053318680802665`, 11.681725473586834`}, 326 -> {13.599665186723309`, 13.913411478922221`}, 327 -> {13.206638648919307`, 13.611568363715937`}, 328 -> {15.964025084302046`, 12.437763763290203`}, 329 -> {15.879660184723864`, 12.975757709099902`}, 330 -> {15.063345419548842`, 10.884947492263498`}, 331 -> {15.685740948673963`, 11.87605782708162}, 332 -> {15.473903683401963`, 14.131522176201079`}, 333 -> {14.824854128177078`, 13.277775910668964`}, 334 -> {15.843899555241505`, 13.222751891117822`}, 335 -> {15.866748963100388`, 14.064873621759856`}, 336 -> {10.539515601522258`, 10.736083576325125`}, 337 -> {10.69217712744977, 9.870853269221179}, 338 -> {11.353558163516919`, 10.84749310974494}, 339 -> {10.807868574044901`, 11.115608281300398`}, 340 -> {9.910791185906254, 8.471554371360828}, 341 -> {9.81674485140098, 7.458338716272725}, 342 -> {10.343937905749836`, 9.636778001527034}, 343 -> {10.381868998990665`, 9.050237577124888}, 344 -> {12.41949553553432, 13.217166381858704`}, 345 -> {11.98858619482119, 12.867976102044347`}, 346 -> {12.793102515365659`, 11.688616633903356`}, 347 -> {12.717644117531934`, 12.80171383221538}, 348 -> {11.293886970987833`, 12.154629568258134`}, 349 -> {11.490934832783095`, 11.025021876302393`}, 350 -> {11.761067418947992`, 12.79926724681619}, 351 -> {11.349045510671221`, 12.687467132591909`}, 352 -> {20.271333966192564`, 8.965054985781368}, 353 -> {20.017994266889904`, 9.431542268718125}, 354 -> {18.58007983465817, 8.669735024015566}, 355 -> {19.831648086830224`, 8.688309199914528}, 356 -> {19.371181719352613`, 10.226716206373217`}, 357 -> {18.15666848731374, 9.952781985561844}, 358 -> {19.95955227844548, 9.678947900571814}, 359 -> {19.93963187238929, 10.165168746557603`}, 360 -> {16.9754496564222, 8.128175808716808}, 361 -> {17.690540805624703`, 7.938331109066248}, 362 -> {15.294013315469536`, 7.8064804765721}, 363 -> {16.351913384908848`, 8.142568913644304}, 364 -> {19.233838065215764`, 8.069650939471318}, 365 -> {18.52744106181223, 8.45711406832441}, 366 -> {17.94706599559249, 7.716174422101309}, 367 -> {19.01076359679024, 7.762793335484749}, 368 -> {18.012014634123624`, 13.071090308299082`}, 369 -> {17.178834911068172`, 12.517927971159649`}, 370 -> {18.040920471452665`, 12.026593061522496`}, 371 -> {18.356564488537824`, 12.893818139690165`}, 372 -> {16.22909963576365, 11.410420500846277`}, 373 -> {15.31146758508006, 10.665204724732103`}, 374 -> {17.079303375541397`, 12.286693759604645`}, 375 -> {16.52596719073692, 12.062912132605911`}, 376 -> {19.711373014297575`, 11.095217353036368`}, 377 -> {19.616045810902985`, 11.553419604924184`}, 378 -> {18.064123413287525`, 10.211892524095667`}, 379 -> {19.21908532404918, 10.76468980039723}, 380 -> {19.189773610057667`, 12.54685054799994}, 381 -> {18.20169216629831, 11.874156157100648`}, 382 -> {19.56353841558557, 11.801197463442174`}, 383 -> {19.661503798202045`, 12.442760194265137`}, 384 -> {1.8691816327553177`, 1.3485549659186007`}, 385 -> {1.8350504470156195`, 2.007617492175618}, 386 -> {3.1638170078886945`, 2.2015828502111323`}, 387 -> {2.3452420935715534`, 1.3448388126387132`}, 388 -> {1.9415843651588613`, 3.1090105298952655`}, 389 -> {2.9697760677783567`, 3.8540918530132515`}, 390 -> {1.7290466326210419`, 2.2383649855449206`}, 391 -> {1.5395697079182664`, 2.6745554088481938`}, 392 -> {4.6533852262381945`, 2.421444941760983}, 393 -> {4.428294464229643, 1.8757900213418517`}, 394 -> {5.726862116828631, 3.895085909758719}, 395 -> {4.9434616156505795`, 3.0652596700205716`}, 396 -> {3.18696760672239, 1.1672353668289361`}, 397 -> {3.3599230900922397`, 2.072708582869418}, 398 -> {4.24744629741511, 1.727889870583832}, 399 -> {3.5515313773913215`, 1.042667295929156}, 400 -> {1.6742264099775213`, 6.073368558721967}, 401 -> {2.7043168989694757`, 6.274588824348263}, 402 -> {2.151039350286135, 5.489258663763903}, 403 -> {1.4504495442771432`, 5.7714864204415015`}, 404 -> {4.044579800391335, 6.780480198052568}, 405 -> {4.979067829480787, 7.068945248071374}, 406 -> {2.9760627945127127`, 6.334292931424521}, 407 -> {3.571153530749396, 6.734180538539314}, 408 -> {1.1366453803236276`, 3.5426435743933498`}, 409 -> {1.0166299143230686`, 4.0198404277362325`}, 410 -> {2.826646089938228, 4.092006347730651}, 411 -> {1.6870973179124706`, 3.608121573846643}, 412 -> {0.9205205258976232, 5.017318238906172}, 413 -> {2.1274697748558054`, 5.2702113806623485`}, 414 -> {0.9051824247985466, 4.24666287049311}, 415 -> {0.5611423499014171, 4.646921276784331}, 416 -> {10.099865524673385`, 2.2794275943074784`}, 417 -> {9.673358595581615, 2.104422614791816}, 418 -> {9.96549298576773, 3.844051424303155}, 419 -> {10.127874814555595`, 2.8084443519564966`}, 420 -> {8.698222676229491, 1.9583179480369077`}, 421 -> {8.39229031741017, 3.0219895183195127`}, 422 -> {9.45318019395323, 1.9777415640788696`}, 423 -> {9.07132019146989, 1.5852969953910043`}, 424 -> {9.235183543941597, 6.053713506908798}, 425 -> {9.337603025859355, 5.478313744978044}, 426 -> {9.93661677764339, 7.014022968836638}, 427 -> {9.349693369734098, 6.517788760961554}, 428 -> {9.713077143496962, 4.0504811728926065`}, 429 -> {9.525709013595574, 3.890021534231551}, 430 -> {9.698322748832087, 5.143992500616164}, 431 -> {9.205878149911355, 4.4755001420855125`}, 432 -> {5.7359413247867375`, 0.4343489838434571}, 433 -> {5.654166733806448, 1.290219667502146}, 434 -> {6.638401968898531, 1.311090600168602}, 435 -> {6.129740655501775, 0.3960966802625739}, 436 -> {5.589631998536661, 2.6741081865753795`}, 437 -> {6.004581742175376, 3.7041826753091947`}, 438 -> {5.592851331266756, 1.530294261691186}, 439 -> {5.438575772376027, 2.067001155507924}, 440 -> {8.284188595347134, 1.1601256004389766`}, 441 -> {7.951074572156767, 0.812831057324171}, 442 -> {8.120557268536858, 3.022254705062173}, 443 -> {8.156124093334014, 1.7848372437696274`}, 444 -> {6.9371707767110165`, 0.1829491044719979}, 445 -> {6.879215881658812, 1.2425427816655097`}, 446 -> {7.766258569438685, 0.6617753107831408}, 447 -> {7.313585100581754, 0.}, 448 -> {5.04869493462184, 14.83449335237893}, 449 -> {5.809759326621639, 14.449049019361253`}, 450 -> {4.961968278008819, 13.557116312030477`}, 451 -> {4.839220020491851, 14.627732469343025`}, 452 -> {6.545845420457402, 13.50810105442593}, 453 -> {6.841027201049091, 12.272540483001324`}, 454 -> {6.053423484434542, 14.37293804138501}, 455 -> {6.491901973437757, 14.146350635140905`}, 456 -> {4.026636636201488, 12.415762845489663`}, 457 -> {3.998398486279803, 12.961242802482735`}, 458 -> {5.007478752552797, 10.985252415420348`}, 459 -> {4.298712063071606, 11.876244526937803`}, 460 -> {4.1961070846993875`, 14.212784877885971`}, 461 -> {5.095683834505322, 13.553673390393305`}, 462 -> {3.9812557926031293`, 13.215866651388081`}, 463 -> {3.8175648602486594`, 14.061509353265993`}, 464 -> {9.125827093588358, 11.922486052676081`}, 465 -> {9.061735982879188, 10.933451380321861`}, 466 -> {8.399503751024763, 11.869595123369843`}, 467 -> {8.93669180773256, 12.297712061583267`}, 468 -> {8.939391244748885, 9.300504773880995}, 469 -> {9.51666999761663, 8.661222306971224}, 470 -> {8.775233306128918, 10.526257219045839`}, 471 -> {8.763349704481925, 9.860026741851756}, 472 -> {7.311637969140107, 14.006748555072383`}, 473 -> {7.786038141043108, 13.794557509700095`}, 474 -> {7.094564980176753, 12.351710920780096`}, 475 -> {7.08311526807237, 13.506512296066504`}, 476 -> {8.595126156207895, 13.258433819231023`}, 477 -> {8.487572209526506, 12.098315797992662`}, 478 -> {8.027855227306466, 13.777802038666199`}, 479 -> {8.461303369749228, 13.794811193287696`}, 480 -> {0., 8.584711542046655}, 481 -> {0.2315840680449847, 9.074946057690713}, 482 -> {1.6602856973190303`, 8.376785979964792}, 483 -> {0.432726776153617, 8.309671088986978}, 484 -> {0.8108100010167437, 9.902516943244855}, 485 -> {2.038536606469143, 9.73892995462091}, 486 -> {0.2740524971939218, 9.32621926124448}, 487 -> {0.2586978606893887, 9.822185409024064}, 488 -> {3.423522294656324, 7.903537791274507}, 489 -> {2.736669489441854, 7.687862691832968}, 490 -> {4.957266180054222, 7.521652113634507}, 491 -> {4.015151241298495, 7.877531283522981}, 492 -> {1.1394064761365559`, 7.686732577603331}, 493 -> {1.7235256440313997`, 8.155713913233994}, 494 -> {2.490438145740976, 7.4480261116268585`}, 495 -> {1.44403805155787, 7.426136248115918}, 496 -> {1.9446639190603052`, 12.870982198923288`}, 497 -> {2.812962937977876, 12.405839731456009`}, 498 -> {2.0107199966513436`, 11.829640359919038`}, 499 -> {1.6092757956978183`, 12.659647129205103`}, 500 -> {3.8309880729961323`, 11.311532736452628`}, 501 -> {4.800223462881658, 10.719327086016616`}, 502 -> {2.9248053701942744`, 12.166805969522446`}, 503 -> {3.5169690003440515`, 11.982468029981806`}, 504 -> {0.4260111483947995, 10.786199556812807`}, 505 -> {0.4945906960609432, 11.256898557240332`}, 506 -> {2.1150709137435983`, 10.008111049422984`}, 507 -> {0.9278892696960458, 10.456892480178393`}, 508 -> {0.837232159951649, 12.265975635522503`}, 509 -> {1.8468659822786633`, 11.658842359375146`}, 510 -> {0.5250360486360477, 11.510247416767399`}, 511 -> {0.38828423539169743`, 12.152892107955374`}, 0 -> {10.442689267558638`, 6.31987316116378}, 2 -> {15.09470267003398, 7.477569869398714}, 4 -> {15.12051055228951, 4.343034226957801}, 5 -> {14.276428773708833`, 10.50425133256849}, 8 -> {17.718950108322268`, 5.210534696477989}, 9 -> {13.222839635954195`, 3.1825444001396086`}, 10 -> {12.133909172329147`, 11.049855771960384`}, 11 -> {17.002269718660582`, 10.365113890441151`}, 16 -> {17.881156825169196`, 3.5818921513858832`}, 17 -> {18.010862372901883`, 6.585819708251272}, 18 -> {11.845423351513448`, 3.581690899884297}, 19 -> {15.133821813755326`, 2.0794584806481993`}, 20 -> {13.645447728028815`, 12.647743877632976`}, 21 -> {10.911748892865683`, 10.202133228861133`}, 22 -> {17.63151145179777, 9.13650000277134}, 23 -> {16.72222620868384, 11.975542062879345`}, 32 -> {19.139725537637027`, 3.8488602880204184`}, 33 -> {17.11848442640882, 3.173785146337737}, 34 -> {17.271491637904887`, 7.224455421553898}, 35 -> {19.318986937358737`, 5.735768202616322}, 36 -> {12.641751598463227`, 2.0297350030924086`}, 37 -> {11.325147705047762`, 4.523367354693979}, 38 -> {15.984291576223509`, 2.4060423762041303`}, 39 -> {14.459470095316371`, 1.3849966380765206`}, 40 -> {12.807039678821297`, 13.095850992770869`}, 41 -> {14.562829871109654`, 12.583069222951456`}, 42 -> {10.842942578700248`, 9.102519295126243}, 43 -> {11.258364153754654`, 11.858612497810837`}, 44 -> {18.677367277483377`, 10.294040902930686`}, 45 -> {17.076579089075384`, 8.352401258845742}, 46 -> {15.873926304882076`, 12.189744621018113`}, 47 -> {18.006912295404017`, 12.045399601555047`}, 64 -> {19.333824303836586`, 3.090551286198032}, 65 -> {19.201313244394427`, 4.4000799871835685`}, 66 -> {16.481202403670018`, 3.4710286437887916`}, 67 -> {18.256534916572637`, 2.6335368676644073`}, 68 -> {18.57596299570538, 7.103655811251}, 69 -> {16.511076704130506`, 7.193346524158764}, 70 -> {19.333123490579474`, 5.167064942289278}, 71 -> {19.599892670192624`, 6.298236375159085}, 72 -> {12.13656294442011, 2.0255110720296887`}, 73 -> {13.22999684688563, 1.7742877684133713`}, 74 -> {11.292686683641112`, 5.332315331729209}, 75 -> {11.60110469356648, 3.324704424426928}, 76 -> {16.147751510583866`, 1.3651767640207133`}, 77 -> {15.97829650526958, 3.0567789986458767`}, 78 -> {13.941181369587802`, 1.6652022175303376`}, 79 -> {15.275537176059274`, 0.7979865518640796}, 80 -> {13.382283012438116`, 13.91290533622735}, 81 -> {12.414094080240254`, 12.670287404686508`}, 82 -> {14.746456042745937`, 11.959359940599159`}, 83 -> {14.427623963892028`, 13.615440749719554`}, 84 -> {11.052955636990593`, 10.120359665303674`}, 85 -> {10.9041832399894, 8.388665358206183}, 86 -> {11.74662363816568, 12.322998303434474`}, 87 -> {10.768630189486707`, 11.656573150165489`}, 88 -> {19.0895771160776, 9.829998749652479}, 89 -> {18.541311420583263`, 10.839439828955797`}, 90 -> {16.390962025910973`, 7.970649368197537}, 91 -> {18.29375546004645, 8.830326351725105}, 92 -> {16.834546669322204`, 12.997595696345407`}, 93 -> {15.367486114457087`, 11.71416045580581}, 94 -> {18.21749201260525, 11.534630282818078`}, 95 -> {17.990820365445458`, 12.828244953889072`}, 128 -> {19.917288781579117`, 3.108372316854343}, 129 -> {19.036509223658975`, 2.951004643514379}, 130 -> {18.869699805406476`, 4.68219035538398}, 131 -> {19.886440090694002`, 3.8726621393964766`}, 132 -> {17.297999905975594`, 2.919675395240551}, 133 -> {16.110760554447808`, 3.8450197449072103`}, 134 -> {18.641460184527805`, 2.707502941005414}, 135 -> {18.06799168567715, 2.364583733706329}, 136 -> {18.419014531749013`, 7.340689007747306}, 137 -> {18.970841465243375`, 6.901045782611283}, 138 -> {15.99945009237134, 7.203295146370655}, 139 -> {17.40211521365483, 7.072904929364348}, 140 -> {20.073904374813367`, 5.305777417595625}, 141 -> {18.955227638958817`, 5.049719084678584}, 142 -> {19.31532049141498, 6.51081013001459}, 143 -> {20.22198404322763, 5.995356944486861}, 144 -> {12.392518919807948`, 1.3094321345236466`}, 145 -> {12.024163270659757`, 2.3780280919837917`}, 146 -> {13.449007484788318`, 2.095251331737183}, 147 -> {13.043249549548023`, 1.1977885987645127`}, 148 -> {11.685273489264087`, 4.703542274880975}, 149 -> {11.192014703753488`, 5.82675758900649}, 150 -> {11.885992031484962`, 2.8847966993409617`}, 151 -> {11.468505024349527`, 3.576633861494477}, 152 -> {16.554430031636247`, 1.3652768134124322`}, 153 -> {15.896490076772391`, 1.137466459096819}, 154 -> {15.813589716917196`, 3.513320114067195}, 155 -> {16.412146766449702`, 2.2604136808511353`}, 156 -> {14.348082071473753`, 0.8261107800140177}, 157 -> {13.804131167945709`, 2.118085182016923}, 158 -> {15.573709211128602`, 0.9227048946103302}, 159 -> {15.082057063872167`, 0.396552171470681}, 160 -> {13.083513588849023`, 14.230451552923835`}, 161 -> {13.703994947217662`, 13.873995794888232`}, 162 -> {12.410760193711841`, 12.202084290385155`}, 163 -> {12.581277012178942`, 13.577691693284565`}, 164 -> {14.950180964405877`, 12.83899298819642}, 165 -> {14.709415564610211`, 11.46898970039913}, 166 -> {14.134469778119154`, 13.76393149209127}, 167 -> {14.818970305215025`, 13.731801954295177`}, 168 -> {11.149770086401722`, 9.845882179261068}, 169 -> {11.087380379538926`, 10.647169600159202`}, 170 -> {10.857274621304159`, 7.997935562573488}, 171 -> {11.16417118715839, 8.953331960316742}, 172 -> {11.421528220437024`, 12.772465310680873`}, 173 -> {12.054023815135057`, 12.112975509077934`}, 174 -> {10.668892796170255`, 11.287738167635906`}, 175 -> {10.83073017597056, 12.383762172163319`}, 176 -> {19.615071127156263`, 10.285240416598043`}, 177 -> {18.85909747891801, 9.559706287873691}, 178 -> {18.145997208040995`, 10.85191241843622}, 179 -> {19.292437015134794`, 10.897293092897794`}, 180 -> {17.22385476358185, 8.25054472859174}, 181 -> {15.9543021107151, 7.825576635623123}, 182 -> {18.624014200422792`, 9.125793220223319}, 183 -> {18.2047062493165, 8.57684083055572}, 184 -> {16.58685795794767, 13.219504324170616`}, 185 -> {17.22451268947659, 13.02032892871572}, 186 -> {15.10941201315001, 11.24325243967555}, 187 -> {15.905611531897447`, 12.557396214953805`}, 188 -> {18.734257924881625`, 12.223033113330931`}, 189 -> {17.96706677510558, 11.181762851800475`}, 190 -> {17.666061955806775`, 12.88331172477762}, 191 -> {18.55686467728411, 12.960467431248404`}}], ResourceFunction["WolframModelPlot"][ ResourceFunction[ "WolframModel"][{{x, y}} -> {{z, y, x}, {y, z}, {z, x}}, {{0, 0}}, 9, "FinalState"], "MaxImageSize" -> 100, VertexCoordinateRules -> { 1 -> {10.17470974389601, 8.49613742700209}, 3 -> {5.522696341420668, 7.338440718767156}, 6 -> {6.3409702377458155`, 4.311759255597379}, 7 -> {5.496888459165139, 10.472976361208069`}, 12 -> {3.615129292794065, 4.450896697724719}, 13 -> {8.4834898391255, 3.766154816205485}, 14 -> {7.394559375500452, 11.633466188026262`}, 15 -> {2.8984489031323792`, 9.605475891687881}, 24 -> {3.895172802770809, 2.840468525286524}, 25 -> {2.985887559656875, 5.67951058539453}, 26 -> {9.705650118588965, 4.6138773593047375`}, 27 -> {6.971951283425833, 2.168266710532894}, 28 -> {5.483577197699321, 12.73655210751767}, 29 -> {8.7719756599412, 11.234319688281573`}, 30 -> {2.6065366385527637`, 8.230190879914598}, 31 -> {2.7362421862854522`, 11.234118436779987`}, 48 -> {2.6104867160506307`, 2.770610986610823}, 49 -> {4.743472706572571, 2.6262659671477575`}, 50 -> {3.540819922379263, 6.463609329320128}, 51 -> {1.9400317339712698`, 4.5219696852351845`}, 52 -> {9.359034857699994, 2.9573980903550328`}, 53 -> {9.7744564327544, 5.7134912930396275`}, 54 -> {6.054569140344993, 2.2329413652144137`}, 55 -> {7.810359332633349, 1.7201595953950017`}, 56 -> {6.157928916138276, 13.43101395008935}, 57 -> {4.63310743523114, 12.40996821196174}, 58 -> {9.292251306406886, 10.29264323347189}, 59 -> {7.975647412991421, 12.786275585073462`}, 60 -> {1.298412074095909, 9.080242385549548}, 61 -> {3.3459073735497626`, 7.591555166611972}, 62 -> {3.4989145850458265`, 11.642225441828133`}, 63 -> {1.4776734738176203`, 10.967150300145452`}, 96 -> {2.6265786460091918`, 1.9877656342767989`}, 97 -> {2.3999069988493984`, 3.2813803053477923`}, 98 -> {5.249912896997562, 3.1018501323600587`}, 99 -> {3.7828523421324425`, 1.8184148918204628`}, 100 -> {2.3236435514081957`, 5.985684236440766}, 101 -> {4.226436985543674, 6.845361219968333}, 102 -> {2.0760875908713823`, 3.9765707592100723`}, 103 -> {1.527821895377047, 4.9860118385133925`}, 104 -> {9.84876882196794, 3.159437438000381}, 105 -> {8.870775373288968, 2.4930122847313956`}, 106 -> {9.713215771465247, 6.4273452299596885`}, 107 -> {9.564443374464055, 4.695650922862196}, 108 -> {6.189775047562619, 1.2005698384463175`}, 109 -> {5.870942968708712, 2.856650647566711}, 110 -> {8.203304931214394, 2.1457231834793618`}, 111 -> {7.235115999016531, 0.9031052519385188}, 112 -> {5.341861835395375, 14.01802403630179}, 113 -> {6.676217641866845, 13.150808370635533`}, 114 -> {4.639102506185069, 11.759231589519993`}, 115 -> {4.46964750087078, 13.450833824145157`}, 116 -> {9.016294317888168, 11.491306163738942`}, 117 -> {9.324712327813536, 9.483695256436661}, 118 -> {7.387402164569019, 13.041722819752499`}, 119 -> {8.480836067034538, 12.790499516136181`}, 120 -> {1.0175063412620267`, 8.517774213006785}, 121 -> {1.2842755208751715`, 9.648945645876593}, 122 -> {4.106322307324142, 7.622664064007106}, 123 -> {2.041436015749269, 7.71235477691487}, 124 -> {2.360864094882011, 12.182473720501463`}, 125 -> {4.136196607784628, 11.344981944377079`}, 126 -> {1.4160857670602205`, 10.415930600982302`}, 127 -> {1.2835747076180641`, 11.725459301967838`}, 192 -> {2.0605343341705344`, 1.855543156917466}, 193 -> {2.951337055647875, 1.9326988633882491`}, 194 -> {2.6503322363490667`, 3.634247736365396}, 195 -> {1.8831410865730231`, 2.592977474834938}, 196 -> {4.7117874795572, 2.258614373212065}, 197 -> {5.507986998304639, 3.5727581484903213`}, 198 -> {3.3928863219780556`, 1.7956816594501495`}, 199 -> {4.030541053506976, 1.5965062639952539`}, 200 -> {2.4126927621381484`, 6.239169757610148}, 201 -> {1.993384811031858, 5.6902173679425525`}, 202 -> {4.663096900739548, 6.990433952542747}, 203 -> {3.3935442478727955`, 6.565465859574131}, 204 -> {1.324961996319851, 3.9187174952680772`}, 205 -> {2.4714018034136513`, 3.964098169729651}, 206 -> {1.7583015325366371`, 5.256304300292178}, 207 -> {1.0023278842983847`, 4.530770171567826}, 208 -> {9.786668835484088, 2.432248416002552}, 209 -> {9.948506215284393, 3.5282724205299636`}, 210 -> {8.56337519631959, 2.703035079087936}, 211 -> {9.195870791017624, 2.043545277484997}, 212 -> {9.453227824296258, 5.862678627849127}, 213 -> {9.760124390150489, 6.818075025592382}, 214 -> {9.530018631915722, 4.168840988006668}, 215 -> {9.467628925052926, 4.9701284089048015`}, 216 -> {5.798428706239622, 1.0842086338706933`}, 217 -> {6.482929233335493, 1.052079096074601}, 218 -> {5.907983446844438, 3.347020887766741}, 219 -> {5.66721804704877, 1.9770175999694504`}, 220 -> {8.036121999275705, 1.2383188948813042`}, 221 -> {8.206638817742807, 2.613926297780714}, 222 -> {6.913404064236986, 0.9420147932776375}, 223 -> {7.533885422605626, 0.5855590352420348}, 224 -> {5.53534194758248, 14.41945841669519}, 225 -> {5.043689800326046, 13.89330569355554}, 226 -> {6.813267843508938, 12.697925406148947`}, 227 -> {6.269316939980895, 13.989899808151852`}, 228 -> {4.205252245004947, 12.555596907314735`}, 229 -> {4.8038092945374515`, 11.302690474098675`}, 230 -> {4.720908934682256, 13.678544129069051`}, 231 -> {4.0629689798184, 13.450733774753438`}, 232 -> {9.14889398710512, 11.239376726671393`}, 233 -> {8.731406979969686, 11.931213888824908`}, 234 -> {9.42538430770116, 8.98925299915938}, 235 -> {8.93212552219056, 10.112468313284895`}, 236 -> {7.574149461906626, 13.618221989401357`}, 237 -> {7.168391526666329, 12.720759256428687`}, 238 -> {8.59323574079489, 12.437982496182078`}, 239 -> {8.2248800916467, 13.506578453642224`}, 240 -> {0.3954149682270211, 8.820653643679009}, 241 -> {1.3020785200396694`, 8.30520045815128}, 242 -> {1.6621713724958307`, 9.766291503487286}, 243 -> {0.5434946366412812, 9.510233170570245}, 244 -> {3.215283797799815, 7.743105658801523}, 245 -> {4.617948919083308, 7.612715441795215}, 246 -> {1.6465575462112751`, 7.914964805554587}, 247 -> {2.1983844797056356`, 7.475321580418564}, 248 -> {2.549407325777497, 12.451426854459541`}, 249 -> {1.9759388269268425`, 12.108507647160456`}, 250 -> {4.506638457006838, 10.97099084325866}, 251 -> {3.3193991054790533`, 11.896335192925319`}, 252 -> {0.7309589207606464, 10.943348448769393`}, 253 -> {1.7476992060481733`, 10.13382023278189}, 254 -> {1.5808897877956716`, 11.865005944651491`}, 255 -> {0.7001102298755331, 11.707638271311527`}, 384 -> {1.8691816327553177`, 1.3485549659186007`}, 385 -> {1.8350504470156195`, 2.007617492175618}, 386 -> {3.1638170078886945`, 2.2015828502111323`}, 387 -> {2.3452420935715534`, 1.3448388126387132`}, 388 -> {1.9415843651588613`, 3.1090105298952655`}, 389 -> {2.9697760677783567`, 3.8540918530132515`}, 390 -> {1.7290466326210419`, 2.2383649855449206`}, 391 -> {1.5395697079182664`, 2.6745554088481938`}, 392 -> {4.6533852262381945`, 2.421444941760983}, 393 -> {4.428294464229643, 1.8757900213418517`}, 394 -> {5.726862116828631, 3.895085909758719}, 395 -> {4.9434616156505795`, 3.0652596700205716`}, 396 -> {3.18696760672239, 1.1672353668289361`}, 397 -> {3.3599230900922397`, 2.072708582869418}, 398 -> {4.24744629741511, 1.727889870583832}, 399 -> {3.5515313773913215`, 1.042667295929156}, 400 -> {1.6742264099775213`, 6.073368558721967}, 401 -> {2.7043168989694757`, 6.274588824348263}, 402 -> {2.151039350286135, 5.489258663763903}, 403 -> {1.4504495442771432`, 5.7714864204415015`}, 404 -> {4.044579800391335, 6.780480198052568}, 405 -> {4.979067829480787, 7.068945248071374}, 406 -> {2.9760627945127127`, 6.334292931424521}, 407 -> {3.571153530749396, 6.734180538539314}, 408 -> {1.1366453803236276`, 3.5426435743933498`}, 409 -> {1.0166299143230686`, 4.0198404277362325`}, 410 -> {2.826646089938228, 4.092006347730651}, 411 -> {1.6870973179124706`, 3.608121573846643}, 412 -> {0.9205205258976232, 5.017318238906172}, 413 -> {2.1274697748558054`, 5.2702113806623485`}, 414 -> {0.9051824247985466, 4.24666287049311}, 415 -> {0.5611423499014171, 4.646921276784331}, 416 -> {10.099865524673385`, 2.2794275943074784`}, 417 -> {9.673358595581615, 2.104422614791816}, 418 -> {9.96549298576773, 3.844051424303155}, 419 -> {10.127874814555595`, 2.8084443519564966`}, 420 -> {8.698222676229491, 1.9583179480369077`}, 421 -> {8.39229031741017, 3.0219895183195127`}, 422 -> {9.45318019395323, 1.9777415640788696`}, 423 -> {9.07132019146989, 1.5852969953910043`}, 424 -> {9.235183543941597, 6.053713506908798}, 425 -> {9.337603025859355, 5.478313744978044}, 426 -> {9.93661677764339, 7.014022968836638}, 427 -> {9.349693369734098, 6.517788760961554}, 428 -> {9.713077143496962, 4.0504811728926065`}, 429 -> {9.525709013595574, 3.890021534231551}, 430 -> {9.698322748832087, 5.143992500616164}, 431 -> {9.205878149911355, 4.4755001420855125`}, 432 -> {5.7359413247867375`, 0.4343489838434571}, 433 -> {5.654166733806448, 1.290219667502146}, 434 -> {6.638401968898531, 1.311090600168602}, 435 -> {6.129740655501775, 0.3960966802625739}, 436 -> {5.589631998536661, 2.6741081865753795`}, 437 -> {6.004581742175376, 3.7041826753091947`}, 438 -> {5.592851331266756, 1.530294261691186}, 439 -> {5.438575772376027, 2.067001155507924}, 440 -> {8.284188595347134, 1.1601256004389766`}, 441 -> {7.951074572156767, 0.812831057324171}, 442 -> {8.120557268536858, 3.022254705062173}, 443 -> {8.156124093334014, 1.7848372437696274`}, 444 -> {6.9371707767110165`, 0.1829491044719979}, 445 -> {6.879215881658812, 1.2425427816655097`}, 446 -> {7.766258569438685, 0.6617753107831408}, 447 -> {7.313585100581754, 0.}, 448 -> {5.04869493462184, 14.83449335237893}, 449 -> {5.809759326621639, 14.449049019361253`}, 450 -> {4.961968278008819, 13.557116312030477`}, 451 -> {4.839220020491851, 14.627732469343025`}, 452 -> {6.545845420457402, 13.50810105442593}, 453 -> {6.841027201049091, 12.272540483001324`}, 454 -> {6.053423484434542, 14.37293804138501}, 455 -> {6.491901973437757, 14.146350635140905`}, 456 -> {4.026636636201488, 12.415762845489663`}, 457 -> {3.998398486279803, 12.961242802482735`}, 458 -> {5.007478752552797, 10.985252415420348`}, 459 -> {4.298712063071606, 11.876244526937803`}, 460 -> {4.1961070846993875`, 14.212784877885971`}, 461 -> {5.095683834505322, 13.553673390393305`}, 462 -> {3.9812557926031293`, 13.215866651388081`}, 463 -> {3.8175648602486594`, 14.061509353265993`}, 464 -> {9.125827093588358, 11.922486052676081`}, 465 -> {9.061735982879188, 10.933451380321861`}, 466 -> {8.399503751024763, 11.869595123369843`}, 467 -> {8.93669180773256, 12.297712061583267`}, 468 -> {8.939391244748885, 9.300504773880995}, 469 -> {9.51666999761663, 8.661222306971224}, 470 -> {8.775233306128918, 10.526257219045839`}, 471 -> {8.763349704481925, 9.860026741851756}, 472 -> {7.311637969140107, 14.006748555072383`}, 473 -> {7.786038141043108, 13.794557509700095`}, 474 -> {7.094564980176753, 12.351710920780096`}, 475 -> {7.08311526807237, 13.506512296066504`}, 476 -> {8.595126156207895, 13.258433819231023`}, 477 -> {8.487572209526506, 12.098315797992662`}, 478 -> {8.027855227306466, 13.777802038666199`}, 479 -> {8.461303369749228, 13.794811193287696`}, 480 -> {0., 8.584711542046655}, 481 -> {0.2315840680449847, 9.074946057690713}, 482 -> {1.6602856973190303`, 8.376785979964792}, 483 -> {0.432726776153617, 8.309671088986978}, 484 -> {0.8108100010167437, 9.902516943244855}, 485 -> {2.038536606469143, 9.73892995462091}, 486 -> {0.2740524971939218, 9.32621926124448}, 487 -> {0.2586978606893887, 9.822185409024064}, 488 -> {3.423522294656324, 7.903537791274507}, 489 -> {2.736669489441854, 7.687862691832968}, 490 -> {4.957266180054222, 7.521652113634507}, 491 -> {4.015151241298495, 7.877531283522981}, 492 -> {1.1394064761365559`, 7.686732577603331}, 493 -> {1.7235256440313997`, 8.155713913233994}, 494 -> {2.490438145740976, 7.4480261116268585`}, 495 -> {1.44403805155787, 7.426136248115918}, 496 -> {1.9446639190603052`, 12.870982198923288`}, 497 -> {2.812962937977876, 12.405839731456009`}, 498 -> {2.0107199966513436`, 11.829640359919038`}, 499 -> {1.6092757956978183`, 12.659647129205103`}, 500 -> {3.8309880729961323`, 11.311532736452628`}, 501 -> {4.800223462881658, 10.719327086016616`}, 502 -> {2.9248053701942744`, 12.166805969522446`}, 503 -> {3.5169690003440515`, 11.982468029981806`}, 504 -> {0.4260111483947995, 10.786199556812807`}, 505 -> {0.4945906960609432, 11.256898557240332`}, 506 -> {2.1150709137435983`, 10.008111049422984`}, 507 -> {0.9278892696960458, 10.456892480178393`}, 508 -> {0.837232159951649, 12.265975635522503`}, 509 -> {1.8468659822786633`, 11.658842359375146`}, 510 -> {0.5250360486360477, 11.510247416767399`}, 511 -> {0.38828423539169743`, 12.152892107955374`}, 0 -> {10.442689267558638`, 6.31987316116378}, 2 -> {15.09470267003398, 7.477569869398714}, 4 -> {15.12051055228951, 4.343034226957801}, 5 -> {14.276428773708833`, 10.50425133256849}, 8 -> {17.718950108322268`, 5.210534696477989}, 9 -> {13.222839635954195`, 3.1825444001396086`}, 10 -> {12.133909172329147`, 11.049855771960384`}, 11 -> {17.002269718660582`, 10.365113890441151`}, 16 -> {17.881156825169196`, 3.5818921513858832`}, 17 -> {18.010862372901883`, 6.585819708251272}, 18 -> {11.845423351513448`, 3.581690899884297}, 19 -> {15.133821813755326`, 2.0794584806481993`}, 20 -> {13.645447728028815`, 12.647743877632976`}, 21 -> {10.911748892865683`, 10.202133228861133`}, 22 -> {17.63151145179777, 9.13650000277134}, 23 -> {16.72222620868384, 11.975542062879345`}, 32 -> {19.139725537637027`, 3.8488602880204184`}, 33 -> {17.11848442640882, 3.173785146337737}, 34 -> {17.271491637904887`, 7.224455421553898}, 35 -> {19.318986937358737`, 5.735768202616322}, 36 -> {12.641751598463227`, 2.0297350030924086`}, 37 -> {11.325147705047762`, 4.523367354693979}, 38 -> {15.984291576223509`, 2.4060423762041303`}, 39 -> {14.459470095316371`, 1.3849966380765206`}, 40 -> {12.807039678821297`, 13.095850992770869`}, 41 -> {14.562829871109654`, 12.583069222951456`}, 42 -> {10.842942578700248`, 9.102519295126243}, 43 -> {11.258364153754654`, 11.858612497810837`}, 44 -> {18.677367277483377`, 10.294040902930686`}, 45 -> {17.076579089075384`, 8.352401258845742}, 46 -> {15.873926304882076`, 12.189744621018113`}, 47 -> {18.006912295404017`, 12.045399601555047`}, 64 -> {19.333824303836586`, 3.090551286198032}, 65 -> {19.201313244394427`, 4.4000799871835685`}, 66 -> {16.481202403670018`, 3.4710286437887916`}, 67 -> {18.256534916572637`, 2.6335368676644073`}, 68 -> {18.57596299570538, 7.103655811251}, 69 -> {16.511076704130506`, 7.193346524158764}, 70 -> {19.333123490579474`, 5.167064942289278}, 71 -> {19.599892670192624`, 6.298236375159085}, 72 -> {12.13656294442011, 2.0255110720296887`}, 73 -> {13.22999684688563, 1.7742877684133713`}, 74 -> {11.292686683641112`, 5.332315331729209}, 75 -> {11.60110469356648, 3.324704424426928}, 76 -> {16.147751510583866`, 1.3651767640207133`}, 77 -> {15.97829650526958, 3.0567789986458767`}, 78 -> {13.941181369587802`, 1.6652022175303376`}, 79 -> {15.275537176059274`, 0.7979865518640796}, 80 -> {13.382283012438116`, 13.91290533622735}, 81 -> {12.414094080240254`, 12.670287404686508`}, 82 -> {14.746456042745937`, 11.959359940599159`}, 83 -> {14.427623963892028`, 13.615440749719554`}, 84 -> {11.052955636990593`, 10.120359665303674`}, 85 -> {10.9041832399894, 8.388665358206183}, 86 -> {11.74662363816568, 12.322998303434474`}, 87 -> {10.768630189486707`, 11.656573150165489`}, 88 -> {19.0895771160776, 9.829998749652479}, 89 -> {18.541311420583263`, 10.839439828955797`}, 90 -> {16.390962025910973`, 7.970649368197537}, 91 -> {18.29375546004645, 8.830326351725105}, 92 -> {16.834546669322204`, 12.997595696345407`}, 93 -> {15.367486114457087`, 11.71416045580581}, 94 -> {18.21749201260525, 11.534630282818078`}, 95 -> {17.990820365445458`, 12.828244953889072`}, 128 -> {19.917288781579117`, 3.108372316854343}, 129 -> {19.036509223658975`, 2.951004643514379}, 130 -> {18.869699805406476`, 4.68219035538398}, 131 -> {19.886440090694002`, 3.8726621393964766`}, 132 -> {17.297999905975594`, 2.919675395240551}, 133 -> {16.110760554447808`, 3.8450197449072103`}, 134 -> {18.641460184527805`, 2.707502941005414}, 135 -> {18.06799168567715, 2.364583733706329}, 136 -> {18.419014531749013`, 7.340689007747306}, 137 -> {18.970841465243375`, 6.901045782611283}, 138 -> {15.99945009237134, 7.203295146370655}, 139 -> {17.40211521365483, 7.072904929364348}, 140 -> {20.073904374813367`, 5.305777417595625}, 141 -> {18.955227638958817`, 5.049719084678584}, 142 -> {19.31532049141498, 6.51081013001459}, 143 -> {20.22198404322763, 5.995356944486861}, 144 -> {12.392518919807948`, 1.3094321345236466`}, 145 -> {12.024163270659757`, 2.3780280919837917`}, 146 -> {13.449007484788318`, 2.095251331737183}, 147 -> {13.043249549548023`, 1.1977885987645127`}, 148 -> {11.685273489264087`, 4.703542274880975}, 149 -> {11.192014703753488`, 5.82675758900649}, 150 -> {11.885992031484962`, 2.8847966993409617`}, 151 -> {11.468505024349527`, 3.576633861494477}, 152 -> {16.554430031636247`, 1.3652768134124322`}, 153 -> {15.896490076772391`, 1.137466459096819}, 154 -> {15.813589716917196`, 3.513320114067195}, 155 -> {16.412146766449702`, 2.2604136808511353`}, 156 -> {14.348082071473753`, 0.8261107800140177}, 157 -> {13.804131167945709`, 2.118085182016923}, 158 -> {15.573709211128602`, 0.9227048946103302}, 159 -> {15.082057063872167`, 0.396552171470681}, 160 -> {13.083513588849023`, 14.230451552923835`}, 161 -> {13.703994947217662`, 13.873995794888232`}, 162 -> {12.410760193711841`, 12.202084290385155`}, 163 -> {12.581277012178942`, 13.577691693284565`}, 164 -> {14.950180964405877`, 12.83899298819642}, 165 -> {14.709415564610211`, 11.46898970039913}, 166 -> {14.134469778119154`, 13.76393149209127}, 167 -> {14.818970305215025`, 13.731801954295177`}, 168 -> {11.149770086401722`, 9.845882179261068}, 169 -> {11.087380379538926`, 10.647169600159202`}, 170 -> {10.857274621304159`, 7.997935562573488}, 171 -> {11.16417118715839, 8.953331960316742}, 172 -> {11.421528220437024`, 12.772465310680873`}, 173 -> {12.054023815135057`, 12.112975509077934`}, 174 -> {10.668892796170255`, 11.287738167635906`}, 175 -> {10.83073017597056, 12.383762172163319`}, 176 -> {19.615071127156263`, 10.285240416598043`}, 177 -> {18.85909747891801, 9.559706287873691}, 178 -> {18.145997208040995`, 10.85191241843622}, 179 -> {19.292437015134794`, 10.897293092897794`}, 180 -> {17.22385476358185, 8.25054472859174}, 181 -> {15.9543021107151, 7.825576635623123}, 182 -> {18.624014200422792`, 9.125793220223319}, 183 -> {18.2047062493165, 8.57684083055572}, 184 -> {16.58685795794767, 13.219504324170616`}, 185 -> {17.22451268947659, 13.02032892871572}, 186 -> {15.10941201315001, 11.24325243967555}, 187 -> {15.905611531897447`, 12.557396214953805`}, 188 -> {18.734257924881625`, 12.223033113330931`}, 189 -> {17.96706677510558, 11.181762851800475`}, 190 -> {17.666061955806775`, 12.88331172477762}, 191 -> {18.55686467728411, 12.960467431248404`}, 256 -> {20.22911477606295, 2.663118480210496}, 257 -> {20.092362962818598`, 3.305763171398471}, 258 -> {18.770533029175986`, 3.1571682287907237`}, 259 -> {19.780166851502997`, 2.550034952643367}, 260 -> {19.689509741758602`, 4.359118107987477}, 261 -> {18.50232809771105, 4.807899538742886}, 262 -> {20.122808315393705`, 3.5591120309255384`}, 263 -> {20.19138786305985, 4.029811031353063}, 264 -> {17.100430011110596`, 2.833542558184064}, 265 -> {17.692593641260373`, 2.6492046186434237`}, 266 -> {15.81717554857299, 4.096683502149254}, 267 -> {16.786410938458516`, 3.5044778517132418`}, 268 -> {19.00812321575683, 2.156363458960767}, 269 -> {18.606679014803305`, 2.986370228246832}, 270 -> {17.804436073476772`, 2.410170856709861}, 271 -> {18.67273509239434, 1.945028389242582}, 272 -> {19.173360959896776`, 7.3898743400499525`}, 273 -> {18.12696086571367, 7.367984476539012}, 274 -> {18.893873367423247`, 6.660296674931876}, 275 -> {19.477992535318094`, 7.1292780105625395`}, 276 -> {16.602247770156154`, 6.938479304642889}, 277 -> {15.660132831400425`, 7.294358474531363}, 278 -> {17.880729522012793`, 7.128147896332902}, 279 -> {17.19387671679832, 6.912472796891363}, 280 -> {20.35870115076526, 4.9938251791418065`}, 281 -> {20.343346514260723`, 5.48979132692139}, 282 -> {18.578862404985507`, 5.077080633544961}, 283 -> {19.806589010437904`, 4.913493644921015}, 284 -> {20.18467223530103, 6.5063394991788925`}, 285 -> {18.95711331413562, 6.439224608201078}, 286 -> {20.385814943409663`, 5.741064530475157}, 287 -> {20.617399011454648`, 6.231299046119215}, 288 -> {12.15609564170542, 1.021199394878174}, 289 -> {12.589543784148182`, 1.0382085494996716`}, 290 -> {12.129826801928141`, 2.7176947901732085`}, 291 -> {12.022272855246753`, 1.5575767689348474`}, 292 -> {13.534283743382279`, 1.3094982920993665`}, 293 -> {13.522834031277895`, 2.4642996673857738`}, 294 -> {12.83136087041154, 1.0214530784657754`}, 295 -> {13.30576104231454, 0.8092620330934874}, 296 -> {11.854049306972723`, 4.955983846314114}, 297 -> {11.84216570532573, 4.289753369120032}, 298 -> {11.100729013838018`, 6.154788281194646}, 299 -> {11.678007766705763`, 5.515505814284875}, 300 -> {11.680707203722088`, 2.518298526582603}, 301 -> {12.217895260429884`, 2.9464154647960275`}, 302 -> {11.55566302857546, 3.882559207844009}, 303 -> {11.49157191786629, 2.8935245354897887`}, 304 -> {16.79983415120599, 0.7545012348998767}, 305 -> {16.63614321885152, 1.6001439367777888`}, 306 -> {15.521715176949325`, 1.262337197772565}, 307 -> {16.42129192675526, 0.603225710279899}, 308 -> {16.318686948383043`, 2.9397660612280667`}, 309 -> {15.609920258901852`, 3.830758172745522}, 310 -> {16.619000525174844`, 1.8547677856831353`}, 311 -> {16.59076237525316, 2.400247742676207}, 312 -> {14.12549703801689, 0.669659953024965}, 313 -> {14.563975527020105`, 0.4430725467808596}, 314 -> {13.776371810405557`, 2.5434701051645465`}, 315 -> {14.071553590997246`, 1.3079095337399398`}, 316 -> {15.778178990962797`, 0.1882781188228453}, 317 -> {15.65543073344583, 1.2588942761353934`}, 318 -> {14.80763968483301, 0.3669615688046175}, 319 -> {15.568704076832809`, -0.01848276421305961}, 320 -> {13.303813910872893`, 14.81601058816587}, 321 -> {12.851140442015963`, 14.154235277382728`}, 322 -> {13.738183129795836`, 13.57346780650036}, 323 -> {13.68022823474363, 14.633061483693872`}, 324 -> {12.461274918120633`, 13.031173344396244`}, 325 -> {12.49684174291779, 11.793755883103698`}, 326 -> {12.666324439297881`, 14.003179530841699`}, 327 -> {12.333210416107514`, 13.655884987726893`}, 328 -> {15.178823239078621`, 12.749009432657946`}, 329 -> {15.024547680187892`, 13.285716326474684`}, 330 -> {14.612817269279272`, 11.111827912856675`}, 331 -> {15.027767012917987`, 12.14190240159049}, 332 -> {14.487658355952874`, 14.419913907903297`}, 333 -> {13.978997042556117`, 13.504919987997269`}, 334 -> {14.9632322776482, 13.525790920663724`}, 335 -> {14.881457686667911`, 14.381661604322414`}, 336 -> {11.411520861543293`, 10.340510446080359`}, 337 -> {10.91907626262256, 9.672018087549706}, 338 -> {11.091689997859074`, 10.92598905393432}, 339 -> {10.904321867957686`, 10.765529415273264`}, 340 -> {11.26770564172055, 8.298221827204316}, 341 -> {10.680782233811257`, 7.801987619329232}, 342 -> {11.279795985595293`, 9.337696843187826}, 343 -> {11.382215467513051`, 8.762297081257072}, 344 -> {11.546078819984757`, 13.230713592774865`}, 345 -> {11.164218817501418`, 12.838269024087001`}, 346 -> {12.225108694044478`, 11.794021069846357`}, 347 -> {11.919176335225156`, 12.857692640128963`}, 348 -> {10.489524196899053`, 12.007566236209374`}, 349 -> {10.651906025686918`, 10.971959163862715`}, 350 -> {10.944040415873033`, 12.711587973374055`}, 351 -> {10.517533486781263`, 12.536582993858392`}, 352 -> {20.05625666155323, 10.169089311381539`}, 353 -> {19.7122165866561, 10.569347717672759`}, 354 -> {18.48992923659884, 9.54579920750352}, 355 -> {19.696878485557022`, 9.7986923492597}, 356 -> {18.930301693542177`, 11.207889014319228`}, 357 -> {17.79075292151642, 10.72400424043522}, 358 -> {19.60076909713158, 10.796170160429638`}, 359 -> {19.48075363113102, 11.273367013772521`}, 360 -> {17.046245480705252`, 8.081830049626557}, 361 -> {17.641336216941937`, 8.481717656741349}, 362 -> {15.63833118197386, 7.747065340094496}, 363 -> {16.57281921106331, 8.035530390113301}, 364 -> {19.166949467177503`, 9.044524167724369}, 365 -> {18.46635966116851, 9.326751924401968}, 366 -> {17.91308211248517, 8.541421763817606}, 367 -> {18.943172601477126`, 8.742642029443903}, 368 -> {17.065867634063327`, 13.773343292236714`}, 369 -> {16.369952714039538`, 13.088120717582038`}, 370 -> {17.257475921362406`, 12.743302005296453`}, 371 -> {17.430431404732257`, 13.648775221336933`}, 372 -> {15.673937395804067`, 11.750750918145298`}, 373 -> {14.890536894626017`, 10.92092467840715}, 374 -> {16.189104547225003`, 12.940220566824019`}, 375 -> {15.964013785216453`, 12.394565646404887`}, 376 -> {19.077829303536383`, 12.141455179317676`}, 377 -> {18.888352378833606`, 12.577645602620949`}, 378 -> {17.64762294367629, 10.961918735152619`}, 379 -> {18.675814646295784`, 11.707000058270605`}, 380 -> {18.272156917883095`, 13.471171775527157`}, 381 -> {17.453582003565955`, 12.614427737954738`}, 382 -> {18.782348564439026`, 12.808393095990253`}, 383 -> {18.74821737869933, 13.46745562224727}}]}]]

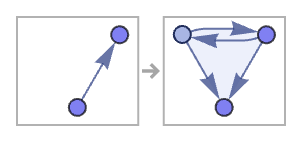
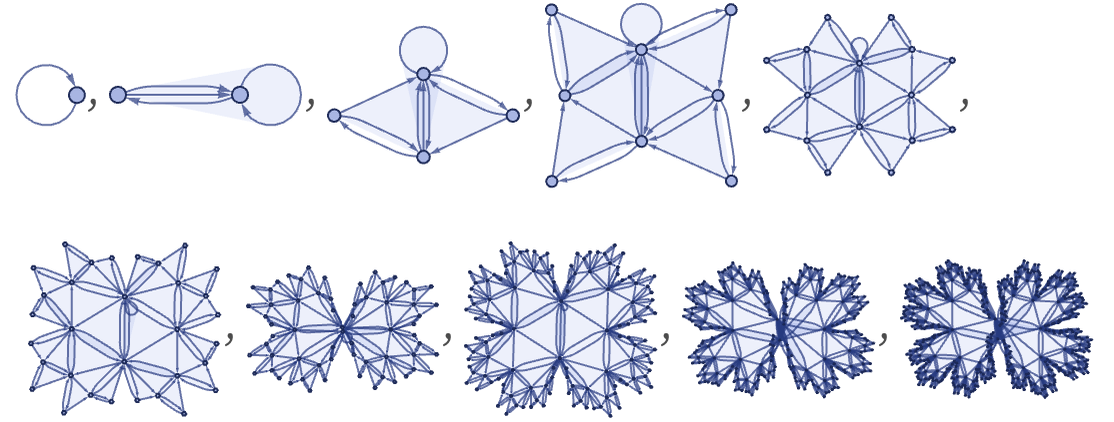
We can think of the structure that is produced as being like a binary tree of triangles:

CloudGet["https://wolfr.am/LDlGWNOC"]; Table[Show[hgraph[k], Overlay3CycleTree[hgraph[k]], ImageSize -> 100], {k, 1, 6}]

The same structure can be produced from an Apollonian circle packing (e.g. [18][1: p985]):

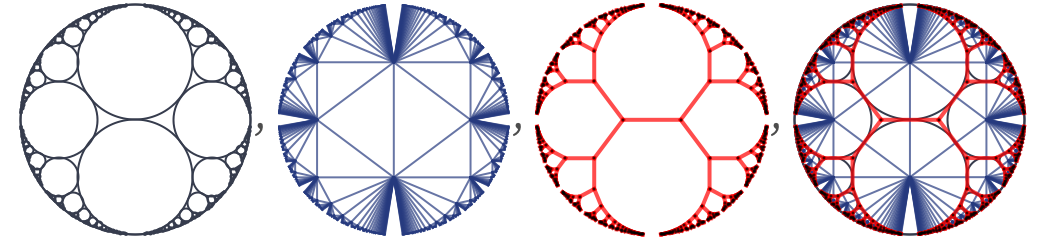
CloudGet["https://wolfr.am/LDlGWNOC"]; Show[#, ImageSize -> 120] & /@ (Append[#, Show[#]] &[ CirclePack[2000]])

If each triangle is required to have the same area, the structure can be rendered in 2D as:

pts = {{0, -1.`20.}, {-1.`20., 0}, {0, 1.`20.}, {1.`20., 0}, { 1.5`20., -1.5`20.}, { 1.5`20., 1.5`20.}, {-1.5`20., 1.5`20.}, {-1.5`20., -1.5`20.}, { 1.12132034355964257320253308631454711785`20., \ -2.70710678118654752440084436210484903928`20.}, { 2.70710678118654752440084436210484903928`20., \ -1.12132034355964257320253308631454711785`20.}, { 2.70710678118654752440084436210484903928`20., 1.12132034355964257320253308631454711785`20.}, { 1.12132034355964257320253308631454711785`20., 2.70710678118654752440084436210484903928`20.}, \ {-1.12132034355964257320253308631454711785`20., 2.70710678118654752440084436210484903928`20.}, \ {-2.70710678118654752440084436210484903928`20., 1.12132034355964257320253308631454711785`20.}, \ {-2.70710678118654752440084436210484903928`20., \ -1.12132034355964257320253308631454711785`20.}, \ {-1.12132034355964257320253308631454711785`20., \ -2.70710678118654752440084436210484903928`20.}, { 0.79419852642987161560934934273958486775`20., \ -3.99270561650904772080251126955401660287`20.}, { 2.46847367459241271032466037638313767368`20., \ -3.69433192638305998443269247571841841951`20.}, { 3.69433192638305998443269247571860510585`20., \ -2.46847367459241271032466037638312913734`20.}, { 3.99270561650904772080251126955401660287`20., \ -0.79419852642987161560934934273960840279`20.}, { 3.99270561650904772080251126955401660287`20., 0.79419852642987161560934934273958486775`20.}, { 3.69433192638305998443269247571860510585`20., 2.46847367459241271032466037638313767368`20.}, { 2.46847367459241271032466037638313767368`20., 3.69433192638305998443269247571860510585`20.}, { 0.79419852642987161560934934273958486775`20., 3.99270561650904772080251126955401660287`20.}, \ {-0.79419852642987161560934934273960840279`20., 3.99270561650904772080251126955401660287`20.}, \ {-2.46847367459241271032466037638312913734`20., 3.69433192638305998443269247571860510585`20.}, \ {-3.69433192638305998443269247571841841951`20., 2.46847367459241271032466037638313767368`20.}, \ {-3.99270561650904772080251126955401660287`20., 0.79419852642987161560934934273958486775`20.}, \ {-3.99270561650904772080251126955401660287`20., \ -0.79419852642987161560934934273960840279`20.}, \ {-3.69433192638305998443269247571841841951`20., \ -2.46847367459241271032466037638312913734`20.}, \ {-2.46847367459241271032466037638312913734`20., \ -3.69433192638305998443269247571841841951`20.}, \ {-0.79419852642987161560934934273960840279`20., \ -3.99270561650904772080251126955401660287`20.}, { 0.55102318312238618372497126620459485886`20., \ -5.59463226576418582728196711338111292191`20.}, { 1.83044317910220187218586706530083656464`20., \ -6.03416248806451987781867073030208119309`20.}, { 2.96120847205624827553663714154394936184`20., \ -5.54003139109315793301630224365458535486`20.}, { 3.78487807448266062413424710532448130705`20., \ -4.61188727767775329761713898646067309991`20.}, { 4.61188727767775329761713899489091891892`20., \ -3.78487807448266062413424710556894732372`20.}, { 5.54003139109315793301630224594187326079`20., \ -2.9612084720562482755366371415424867543`20.}, { 6.03416248806451987781867073030011109744`20., \ -1.83044317910220187218586706530128789947`20.}, { 5.59463226576418582728196711338111292191`20., \ -0.55102318312238618372497126620460635533`20.}, { 5.59463226576418582728196711338111292191`20., 0.55102318312238618372497126620459485886`20.}, { 6.03416248806451987781867073030011109744`20., 1.83044317910220187218586706530083656464`20.}, { 5.54003139109315793301630224594187326079`20., 2.96120847205624827553663714154394936184`20.}, { 4.61188727767775329761713899489091891892`20., 3.78487807448266062413424710532448130705`20.}, { 3.78487807448266062413424710532448130705`20., 4.61188727767775329761713899489091891892`20.}, { 2.96120847205624827553663714154394936184`20., 5.54003139109315793301630224594187326079`20.}, { 1.83044317910220187218586706530083656464`20., 6.03416248806451987781867073030011109744`20.}, { 0.55102318312238618372497126620459485886`20., 5.59463226576418582728196711338111292191`20.}, \ {-0.55102318312238618372497126620460635533`20., 5.59463226576418582728196711338111292191`20.}, \ {-1.83044317910220187218586706530128789947`20., 6.03416248806451987781867073030011109744`20.}, \ {-2.9612084720562482755366371415424867543`20., 5.54003139109315793301630224594187326079`20.}, \ {-3.78487807448266062413424710556894732372`20., 4.61188727767775329761713899489091891892`20.}, \ {-4.61188727767775329761713898646067309991`20., 3.78487807448266062413424710532448130705`20.}, \ {-5.54003139109315793301630224365458535486`20., 2.96120847205624827553663714154394936184`20.}, \ {-6.03416248806451987781867073030208119309`20., 1.83044317910220187218586706530083656464`20.}, \ {-5.59463226576418582728196711338111292191`20., 0.55102318312238618372497126620459485886`20.}, \ {-5.59463226576418582728196711338111292191`20., \ -0.55102318312238618372497126620460635533`20.}, \ {-6.03416248806451987781867073030208119309`20., \ -1.83044317910220187218586706530128789947`20.}, \ {-5.54003139109315793301630224365458535486`20., \ -2.9612084720562482755366371415424867543`20.}, \ {-4.61188727767775329761713898646067309991`20., \ -3.78487807448266062413424710556894732372`20.}, \ {-3.78487807448266062413424710556894732372`20., \ -4.61188727767775329761713898646067309991`20.}, \ {-2.9612084720562482755366371415424867543`20., \ -5.54003139109315793301630224365458535486`20.}, \ {-1.83044317910220187218586706530128789947`20., \ -6.03416248806451987781867073030208119309`20.}, \ {-0.55102318312238618372497126620460635533`20., \ -5.59463226576418582728196711338111292191`20.}, \ {-8.82526348925847426852402385155172376707`17.034535949251175, \ -1.30910417496527758625161316043272474563`17.033641220531187}, \ {-8.60395399378296035339567691607117741313`16.77516083395495, \ -2.15517828152853602905144313192084376115`16.77470680701365}, \ {-7.91791301234602057822105557681832979014`16.781946434870076, \ -2.83307457668812429555399420546063180445`16.781542187064247}, \ {-7.60809348503042668672579049508962667741`16.69360412228167, \ -3.59836023010762696428258572794985579709`16.69333338670229}, \ {-7.71876993056995754333201385207778349273`16.485338827866748, \ -4.6264526527812567562991769980891887432`16.48521426714185}, \ {-7.23113854984243469857080969083717431409`16.47264180519843, \ -5.36297785565941535606411801962901422502`16.472567306844535}, \ {-6.05056443863198370609762787035059609581`16.606920188461768, \ -5.48391194992202377784551399353748118763`16.606876042578037}, \ {-5.48391194992202377784551399353748118763`16.606876042578037, \ -6.05056443863198370609762787035059609581`16.606920188461768}, \ {-5.36297785565941535606411801962901422502`16.472567306844535, \ -7.23113854984243469857080969083717431409`16.47264180519843}, \ {-4.6264526527812567562991769980891887432`16.48521426714185, \ -7.71876993056995754333201385207778349273`16.485338827866748}, \ {-3.59836023010762696428258572794985579709`16.69333338670229, \ -7.60809348503042668672579049508962667741`16.69360412228167}, \ {-2.83307457668812429555399420546063180445`16.781542187064247, \ -7.91791301234602057822105557681832979014`16.781946434870076}, \ {-2.15517828152853602905144313192084376115`16.77470680701365, \ -8.60395399378296035339567691607117741313`16.77516083395495}, \ {-1.30910417496527758625161316043272474563`17.033641220531187, \ -8.82526348925847426852402385155172376707`17.034535949251175}, \ {-0.38525186847282515601338759957429252803`17.65204355589572, \ -7.84198193616441487727518548839545152795`17.655921511225028}, { 0.38525186847282515601338759957428454815`17.65204355589572, \ -7.84198193616441487727518548839545191999`17.655921511225028}, { 1.30910417496527758625161316043269074486`17.03364122053118, \ -8.82526348925847426852402385155172881059`17.034535949251165}, { 2.15517828152853602905144313192052470924`16.77470680701365, \ -8.60395399378296035339567691607125733147`16.77516083395495}, { 2.83307457668812429555399420546036064026`16.781542187064247, \ -7.91791301234602057822105557681842681424`16.781946434870076}, { 3.59836023010762696428258572795063692305`16.69333338670229, \ -7.60809348503042668672579049508925723237`16.69360412228167}, { 4.62645265278125675629917699808998739754`16.485214267141853, \ -7.71876993056995754333201385207730479775`16.485338827866755}, { 5.36297785565941535606411801951449844659`16.472567306844535, \ -7.23113854984243469857080969092210500366`16.47264180519843}, { 5.48391194992202377784551399344165671435`16.606876042578033, \ -6.05056443863198370609762787043744633593`16.60692018846176}, { 6.0505644386319837060976278728085060915`16.606920188461768, \ -5.48391194992202377784551399082559541176`16.606876042578037}, { 7.23113854984243469857080969324094378784`16.47264180519843, \ -5.36297785565941535606411801638790628565`16.472567306844535}, { 7.71876993056995754333201385247488558946`16.485338827866755, \ -4.62645265278125675629917699742666392047`16.485214267141853}, { 7.60809348503042668672579049539844256599`16.69360412228167, \ -3.59836023010762696428258572729691945957`16.69333338670229}, { 7.9179130123460205782210555768182013185`16.781946434870076, \ -2.83307457668812429555399420546099085861`16.781542187064247}, { 8.60395399378296035339567691607107968212`16.775160833954942, \ -2.15517828152853602905144313192123392528`16.774706807013644}, { 8.82526348925847426852402385155172376707`17.034535949251175, \ -1.30910417496527758625161316043272474563`17.033641220531187}, { 7.84198193616441487727518548839545152795`17.655921511225028, \ -0.38525186847282515601338759957429252803`17.65204355589572}, { 7.84198193616441487727518548839545191999`17.655921511225028, 0.38525186847282515601338759957428454815`17.65204355589572}, { 8.82526348925847426852402385155172881059`17.034535949251165, 1.30910417496527758625161316043269074486`17.03364122053118}, { 8.60395399378296035339567691607115960044`16.775160833954942, 2.15517828152853602905144313192091487339`16.774706807013644}, { 7.9179130123460205782210555768182983426`16.781946434870076, 2.83307457668812429555399420546071969444`16.781542187064247}, { 7.6080934850304266867257904953980731209`16.69360412228167, 3.5983602301076269642825857272977005855`16.69333338670229}, { 7.7187699305699575433320138524744068945`16.485338827866755, 4.62645265278125675629917699742746257478`16.485214267141853}, { 7.23113854984243469857080969332587447749`16.47264180519843, 5.36297785565941535606411801627339050715`16.472567306844535}, { 6.05056443863198370609762787289535633164`16.606920188461768, 5.48391194992202377784551399072977093843`16.606876042578037}, { 5.4839119499220237778455139907297709385`16.606876042578033, 6.05056443863198370609762787289535633159`16.60692018846176}, { 5.36297785565941535606411801627339050723`16.472567306844535, 7.23113854984243469857080969332587447747`16.47264180519843}, { 4.62645265278125675629917699742746257478`16.485214267141853, 7.7187699305699575433320138524744068945`16.485338827866755}, { 3.5983602301076269642825857272977005855`16.69333338670229, 7.6080934850304266867257904953980731209`16.69360412228167}, { 2.83307457668812429555399420546071969444`16.781542187064247, 7.9179130123460205782210555768182983426`16.781946434870076}, { 2.15517828152853602905144313192091487339`16.774706807013644, 8.60395399378296035339567691607115960044`16.775160833954942}, { 1.30910417496527758625161316043269074486`17.03364122053118, 8.82526348925847426852402385155172881059`17.034535949251165}, { 0.38525186847282515601338759957428454815`17.65204355589572, 7.84198193616441487727518548839545191999`17.655921511225028}, \ {-0.38525186847282515601338759957429252803`17.65204355589572, 7.84198193616441487727518548839545152795`17.655921511225028}, \ {-1.30910417496527758625161316043272474563`17.033641220531187, 8.82526348925847426852402385155172376707`17.034535949251175}, \ {-2.15517828152853602905144313192123392528`16.774706807013644, 8.60395399378296035339567691607107968212`16.775160833954942}, \ {-2.83307457668812429555399420546099085861`16.781542187064247, 7.9179130123460205782210555768182013185`16.781946434870076}, \ {-3.59836023010762696428258572729691945957`16.69333338670229, 7.60809348503042668672579049539844256599`16.69360412228167}, \ {-4.62645265278125675629917699742666392047`16.485214267141853, 7.71876993056995754333201385247488558946`16.485338827866755}, \ {-5.36297785565941535606411801638790628565`16.472567306844535, 7.23113854984243469857080969324094378784`16.47264180519843}, \ {-5.48391194992202377784551399082559541176`16.606876042578037, 6.0505644386319837060976278728085060915`16.606920188461768}, \ {-6.05056443863198370609762787043744633595`16.606920188461768, 5.48391194992202377784551399344165671428`16.606876042578037}, \ {-7.23113854984243469857080969092210500371`16.47264180519843, 5.36297785565941535606411801951449844654`16.472567306844535}, \ {-7.71876993056995754333201385207730479775`16.485338827866755, 4.62645265278125675629917699808998739754`16.485214267141853}, \ {-7.60809348503042668672579049508925723237`16.69360412228167, 3.59836023010762696428258572795063692305`16.69333338670229}, \ {-7.91791301234602057822105557681842681424`16.781946434870076, 2.83307457668812429555399420546036064026`16.781542187064247}, \ {-8.60395399378296035339567691607125733147`16.77516083395495, 2.15517828152853602905144313192052470924`16.77470680701365}, \ {-8.82526348925847426852402385155172881059`17.034535949251165, 1.30910417496527758625161316043269074486`17.03364122053118}, \ {-7.84198193616441487727518548839545191999`17.655921511225028, 0.38525186847282515601338759957428454815`17.65204355589572}, \ {-7.84198193616441487727518548839545152795`17.655921511225028, \ -0.38525186847282515601338759957429252803`17.65204355589572}, \ {-12.56469391740578813972764281245373316082`15.175269417734073, \ -0.9268275040710143605328471144526960164`15.174308845640514}, \ {-12.40482675629618719564501054647862298771`14.16367260134322, \ -1.52998945170339323305420671803235237454`14.162994360442974}, \ {-11.68689285082893057472440142305424545944`14.278073054080927, \ -2.0278682774862495975101833334004364102`14.277454674050672}, \ {-11.58792252758624789726811803297379676781`14.279214529763525, \ -2.60215502095462160466364024688808977552`14.277833693516131}, \ {-12.27764764922932132051009499560588022822`14.1162981068036, \ -3.39768269419359776465222519756245238052`14.115548618021569}, \ {-12.10004904857511653791637640937476654643`14.13939884018323, \ -3.99731626932698131279112675429804204756`14.138552772560288}, \ {-10.75878228849889555385765042795541222178`14.349253057232684, \ -4.150120289917850605143284948390932898`14.348130809821646}, \ {-10.53915369239631377737704525412081676933`14.348983577901938, \ -4.67168553404962194730838285831785480681`14.347608625900538}, \ {-11.37656781113667374638924644100578119385`14.140573112233579, \ -5.72648300502444805253346221486085229543`14.139876236308433}, \ {-11.0760121335454251550185753807932168553`14.11126530079487, \ -6.27448337180987159549544201545891876377`14.110295811050767}, \ {-10.14660809954495656404848970238296598669`14.257205543307652, \ -6.42526871692760086987596035048691250292`14.256135070526236}, \ {-9.81840110408050676848399471939235549628`14.256942290350468, \ -6.91489823613857446654147883935613498708`14.256037961442951}, \ {-9.94782796131559326410384859048352912607`14.133189485162658, \ -7.76336113793036345049285291956369632611`14.132713127497665}, \ {-9.58585183339442143714093270906628184875`14.175613809696666, \ -8.26881265722017418429656426210364274634`14.175376287305596}, \ {-8.17583709119287599230037827036374163328`14.399709112013559, \ -7.78404400134868895915722180789207543044`14.399577277480127}, \ {-7.78404400134868895915722180789207543044`14.399577277480127, \ -8.17583709119287599230037827036374163328`14.399709112013559}, \ {-8.26881265722017418429656426210364274634`14.175376287305596, \ -9.58585183339442143714093270906628184875`14.175613809696666}, \ {-7.76336113793036345049285291956369632611`14.132713127497665, \ -9.94782796131559326410384859048352912607`14.133189485162658}, \ {-6.91489823613857446654147883935613498708`14.256037961442951, \ -9.81840110408050676848399471939235549628`14.256942290350468}, \ {-6.42526871692760086987596035048691250292`14.256135070526236, \ -10.14660809954495656404848970238296598669`14.257205543307652}, \ {-6.27448337180987159549544201545891876377`14.110295811050767, \ -11.0760121335454251550185753807932168553`14.11126530079487}, \ {-5.72648300502444805253346221486085229543`14.139876236308433, \ -11.37656781113667374638924644100578119385`14.140573112233579}, \ {-4.67168553404962194730838285831785480681`14.347608625900538, \ -10.53915369239631377737704525412081676933`14.348983577901938}, \ {-4.150120289917850605143284948390932898`14.348130809821646, \ -10.75878228849889555385765042795541222178`14.349253057232684}, \ {-3.99731626932698131279112675429804204756`14.138552772560288, \ -12.10004904857511653791637640937476654643`14.13939884018323}, \ {-3.39768269419359776465222519756245238052`14.115548618021569, \ -12.27764764922932132051009499560588022822`14.1162981068036}, \ {-2.60215502095462160466364024688808977552`14.277833693516131, \ -11.58792252758624789726811803297379676781`14.279214529763525}, \ {-2.0278682774862495975101833334004364102`14.277454674050672, \ -11.68689285082893057472440142305424545944`14.278073054080927}, \ {-1.52998945170339323305420671803235237454`14.162994360442974, \ -12.40482675629618719564501054647862298771`14.16367260134322}, \ {-0.9268275040710143605328471144526960164`15.174308845640514, \ -12.56469391740578813972764281245373316082`15.175269417734073}, \ {-0.26947615830614280587481001056424941076`15.452283113143743, \ -10.97724170059084695648658842340215613022`15.457763480020558}, { 0.26947615830614280587481001056424382562`15.452283113143743, \ -10.97724170059084695648658842340215626736`15.457763480020558}, { 0.92682750407101436053284711445267683794`15.174308845640514, \ -12.5646939174057881397276428124537345755`15.175269417734073}, { 1.52998945170339323305420671803231585573`14.162994360442974, \ -12.40482675629618719564501054647862749181`14.16367260134322}, { 2.02786827748624959751018333340038076405`14.277454674050672, \ -11.68689285082893057472440142305425511494`14.278073054080927}, { 2.60215502095462160466364024688784207108`14.277833693516131, \ -11.58792252758624789726811803297385239171`14.279214529763525}, { 3.39768269419359776465222519756180426893`14.115548618021569, \ -12.27764764922932132051009499560605958484`14.1162981068036}, { 3.99731626932698131279112675429742046338`14.138552772560288, \ -12.10004904857511653791637640937497189008`14.13939884018323}, { 4.15012028991785060514328494839074867039`14.348130809821646, \ -10.75878228849889555385765042795548328621`14.349253057232684}, { 4.67168553404962194730838285831839583631`14.347608625900538, \ -10.53915369239631377737704525412057694742`14.348983577901938}, { 5.72648300502444805253346221486260435047`14.139876236308433, \ -11.37656781113667374638924644100489928344`14.140573112233579}, { 6.27448337180987159549544201546062895491`14.110295811050767, \ -11.07601213354542515501857538079224804401`14.11126530079487}, { 6.42526871692760086987596035048744553759`14.256135070526236, \ -10.14660809954495656404848970238262844618`14.257205543307652}, { 6.9148982361385744665414788392783983748`14.256037961442951, \ -9.81840110408050676848399471944710379571`14.256942290350468}, { 7.76336113793036345049285291932738051806`14.132713127497665, \ -9.94782796131559326410384859066795179282`14.133189485162658}, { 8.26881265722017418429656426187592204049`14.175376287305596, \ -9.58585183339442143714093270926271508049`14.175613809696666}, { 7.78404400134868895915722180782733392656`14.399577277480127, \ -8.17583709119287599230037827042538066908`14.399709112013559}, { 8.17583709119287599230037827210816055655`14.399709112013559, \ -7.7840440013486889591572218060598549378`14.399577277480127}, { 9.58585183339442143714093271462545132516`14.175613809696666, \ -8.2688126572201741842965642556590203891`14.175376287305596}, { 9.9478279613155932641038485957029259954`14.133189485162658, \ -7.76336113793036345049285291287565731889`14.132713127497665}, { 9.81840110408050676848399472094211827867`14.256942290350468, \ -6.91489823613857446654147883715564090978`14.256037961442951}, { 10.1466080995449565640484897026587908765`14.257205543307652, \ -6.42526871692760086987596035005133740329`14.256135070526236}, { 11.07601213354542515501857538160097978371`14.11126530079487, \ -6.2744833718098715954954420140330177827`14.110295811050767}, { 11.37656781113667374638924644174296236435`14.140573112233579, \ -5.72648300502444805253346221339632484155`14.139876236308433}, { 10.53915369239631377737704525432128179049`14.348983577901938, \ -4.67168553404962194730838285786561296549`14.347608625900538}, { 10.75878228849889555385765042795531812387`14.349253057232684, \ -4.15012028991785060514328494839117683771`14.348130809821646}, { 12.10004904857511653791637640937449464653`14.13939884018323, \ -3.99731626932698131279112675429886510033`14.138552772560288}, { 12.27764764922932132051009499560564911568`14.1162981068036, \ -3.39768269419359776465222519756328751363`14.115548618021569}, { 11.58792252758624789726811803297373776774`14.279214529763525, \ -2.60215502095462160466364024688835251467`14.277833693516131}, { 11.68689285082893057472440142305424545944`14.278073054080927, \ -2.0278682774862495975101833334004364102`14.277454674050672}, { 12.40482675629618719564501054647862298771`14.16367260134322, \ -1.52998945170339323305420671803235237454`14.162994360442974}, { 12.56469391740578813972764281245373316082`15.175269417734073, \ -0.9268275040710143605328471144526960164`15.174308845640514}, { 10.97724170059084695648658842340215613022`15.457763480020558, \ -0.26947615830614280587481001056424941076`15.452283113143743}, { 10.97724170059084695648658842340215626736`15.457763480020558, 0.26947615830614280587481001056424382562`15.452283113143743}, { 12.5646939174057881397276428124537345755`15.175269417734073, 0.92682750407101436053284711445267683794`15.174308845640514}, { 12.40482675629618719564501054647862749181`14.16367260134322, 1.52998945170339323305420671803231585573`14.162994360442974}, { 11.68689285082893057472440142305425511494`14.278073054080927, 2.02786827748624959751018333340038076405`14.277454674050672}, { 11.58792252758624789726811803297379339164`14.279214529763525, 2.60215502095462160466364024688810481027`14.277833693516131}, { 12.27764764922932132051009499560582847234`14.1162981068036, 3.39768269419359776465222519756263940204`14.115548618021569}, { 12.10004904857511653791637640937469999018`14.13939884018323, 3.99731626932698131279112675429824351615`14.138552772560288}, { 10.7587822884988955538576504279553891883`14.349253057232684, 4.15012028991785060514328494839099261007`14.348130809821646}, { 10.53915369239631377737704525432104196859`14.348983577901938, 4.67168553404962194730838285786615399499`14.347608625900538}, { 11.37656781113667374638924644174208045398`14.140573112233579, 5.72648300502444805253346221339807689655`14.139876236308433}, { 11.07601213354542515501857538160001097241`14.11126530079487, 6.27448337180987159549544201403472797376`14.110295811050767}, { 10.14660809954495656404848970265845333603`14.257205543307652, 6.42526871692760086987596035005187043792`14.256135070526236}, { 9.81840110408050676848399472099686657817`14.256942290350468, 6.91489823613857446654147883707790429736`14.256037961442951}, { 9.94782796131559326410384859588734866218`14.133189485162658, 7.76336113793036345049285291263934151069`14.132713127497665}, { 9.58585183339442143714093271482188455705`14.175613809696666, 8.26881265722017418429656425543129968322`14.175376287305596}, { 8.17583709119287599230037827216979959241`14.399709112013559, 7.78404400134868895915722180599511343379`14.399577277480127}, { 7.78404400134868895915722180599511343388`14.399577277480127, 8.17583709119287599230037827216979959228`14.399709112013559}, { 8.26881265722017418429656425543129968337`14.175376287305596, 9.58585183339442143714093271482188455694`14.175613809696666}, { 7.7633611379303634504928529126393415108`14.132713127497665, 9.94782796131559326410384859588734866214`14.133189485162658}, { 6.91489823613857446654147883707790429747`14.256037961442951, 9.81840110408050676848399472099686657809`14.256942290350468}, { 6.42526871692760086987596035005187043792`14.256135070526236, 10.14660809954495656404848970265845333603`14.257205543307652}, { 6.27448337180987159549544201403472797376`14.110295811050767, 11.07601213354542515501857538160001097241`14.11126530079487}, { 5.72648300502444805253346221339807689655`14.139876236308433, 11.37656781113667374638924644174208045398`14.140573112233579}, { 4.67168553404962194730838285786615399499`14.347608625900538, 10.53915369239631377737704525432104196859`14.348983577901938}, { 4.15012028991785060514328494839099261007`14.348130809821646, 10.7587822884988955538576504279553891883`14.349253057232684}, { 3.99731626932698131279112675429824351615`14.138552772560288, 12.10004904857511653791637640937469999018`14.13939884018323}, { 3.39768269419359776465222519756263940204`14.115548618021569, 12.27764764922932132051009499560582847234`14.1162981068036}, { 2.60215502095462160466364024688810481027`14.277833693516131, 11.58792252758624789726811803297379339164`14.279214529763525}, { 2.02786827748624959751018333340038076405`14.277454674050672, 11.68689285082893057472440142305425511494`14.278073054080927}, { 1.52998945170339323305420671803231585573`14.162994360442974, 12.40482675629618719564501054647862749181`14.16367260134322}, { 0.92682750407101436053284711445267683794`15.174308845640514, 12.5646939174057881397276428124537345755`15.175269417734073}, { 0.26947615830614280587481001056424382562`15.452283113143743, 10.97724170059084695648658842340215626736`15.457763480020558}, \ {-0.26947615830614280587481001056424941076`15.452283113143743, 10.97724170059084695648658842340215613022`15.457763480020558}, \ {-0.9268275040710143605328471144526960164`15.174308845640514, 12.56469391740578813972764281245373316082`15.175269417734073}, \ {-1.52998945170339323305420671803235237454`14.162994360442974, 12.40482675629618719564501054647862298771`14.16367260134322}, \ {-2.0278682774862495975101833334004364102`14.277454674050672, 11.68689285082893057472440142305424545944`14.278073054080927}, \ {-2.60215502095462160466364024688835251467`14.277833693516131, 11.58792252758624789726811803297373776774`14.279214529763525}, \ {-3.39768269419359776465222519756328751363`14.115548618021569, 12.27764764922932132051009499560564911568`14.1162981068036}, \ {-3.99731626932698131279112675429886510033`14.138552772560288, 12.10004904857511653791637640937449464653`14.13939884018323}, \ {-4.15012028991785060514328494839117683771`14.348130809821646, 10.75878228849889555385765042795531812387`14.349253057232684}, \ {-4.67168553404962194730838285786561296549`14.347608625900538, 10.53915369239631377737704525432128179049`14.348983577901938}, \ {-5.72648300502444805253346221339632484155`14.139876236308433, 11.37656781113667374638924644174296236435`14.140573112233579}, \ {-6.2744833718098715954954420140330177827`14.110295811050767, 11.07601213354542515501857538160097978371`14.11126530079487}, \ {-6.42526871692760086987596035005133740329`14.256135070526236, 10.1466080995449565640484897026587908765`14.257205543307652}, \ {-6.91489823613857446654147883715564090978`14.256037961442951, 9.81840110408050676848399472094211827867`14.256942290350468}, \ {-7.76336113793036345049285291287565731889`14.132713127497665, 9.9478279613155932641038485957029259954`14.133189485162658}, \ {-8.2688126572201741842965642556590203891`14.175376287305596, 9.58585183339442143714093271462545132516`14.175613809696666}, \ {-7.7840440013486889591572218060598549378`14.399577277480127, 8.17583709119287599230037827210816055655`14.399709112013559}, \ {-8.17583709119287599230037827042538066914`14.399709112013559, 7.78404400134868895915722180782733392649`14.399577277480127}, \ {-9.58585183339442143714093270926271508056`14.175613809696666, 8.26881265722017418429656426187592204038`14.175376287305596}, \ {-9.94782796131559326410384859066795179289`14.133189485162658, 7.76336113793036345049285291932738051799`14.132713127497665}, \ {-9.81840110408050676848399471944710379574`14.256942290350468, 6.9148982361385744665414788392783983747`14.256037961442951}, \ {-10.14660809954495656404848970238262844618`14.257205543307652, 6.42526871692760086987596035048744553759`14.256135070526236}, \ {-11.07601213354542515501857538079224804401`14.11126530079487, 6.27448337180987159549544201546062895491`14.110295811050767}, \ {-11.37656781113667374638924644100489928344`14.140573112233579, 5.72648300502444805253346221486260435047`14.139876236308433}, \ {-10.53915369239631377737704525412057694742`14.348983577901938, 4.67168553404962194730838285831839583631`14.347608625900538}, \ {-10.75878228849889555385765042795548328621`14.349253057232684, 4.15012028991785060514328494839074867039`14.348130809821646}, \ {-12.10004904857511653791637640937497189008`14.13939884018323, 3.99731626932698131279112675429742046338`14.138552772560288}, \ {-12.27764764922932132051009499560605958484`14.1162981068036, 3.39768269419359776465222519756180426893`14.115548618021569}, \ {-11.58792252758624789726811803297385239171`14.279214529763525, 2.60215502095462160466364024688784207108`14.277833693516131}, \ {-11.68689285082893057472440142305425511494`14.278073054080927, 2.02786827748624959751018333340038076405`14.277454674050672}, \ {-12.40482675629618719564501054647862749181`14.16367260134322, 1.52998945170339323305420671803231585573`14.162994360442974}, \ {-12.5646939174057881397276428124537345755`15.175269417734073, 0.92682750407101436053284711445267683794`15.174308845640514}, \ {-10.97724170059084695648658842340215626736`15.457763480020558, 0.26947615830614280587481001056424382562`15.452283113143743}, \ {-10.97724170059084695648658842340215613022`15.457763480020558, \ -0.26947615830614280587481001056424941076`15.452283113143743}, \ {-17.79762844598512282344705390413118751706`14.22930702954548, \ -0.65552547220153738907967004084784565286`14.212249311922388}, \ {-17.60968320218134674574507427282472788876`14.068791427066426, \ -1.08187470605938232366812507645163314198`14.030008969967259}, \ {-16.65695381793228050808584203667069322301`14.000585243066286, \ -1.43441109943699839870141847779778349598`13.976665623639002}, \ {-16.64677301018509557615239237844633377422`12.803482938529699, \ -1.84609236164073767801421642041098441936`12.783432950664404}, \ {-17.85544245338604434451972861573455047732`12.819676047679714, \ -2.42505974872851272757153351585311094549`12.802700917173786}, \ {-17.79591112573248507455176046713722274677`12.816539964888452, \ -2.86338634623156299512264700209117639533`12.80146817857336}, \ {-16.01519969634362626065689788608629161345`12.735011257229134, \ -2.98179635397777571407074671727131017166`12.724275219282374}, \ {-15.92971359765875718878366413343512754734`12.647711235987842, \ -3.37234623886128944326115482292387787326`12.638018606413388}, \ {-17.52293990237707480842047458025435559075`12.698248087732606, \ -4.16142572435314229176423345359938562086`12.688624706216963}, \ {-17.40503264663657705311663298227568094025`12.46000235611703, \ -4.58743853522097220067597525896540520302`12.45136727422111}, \ {-16.32039786646297999355248712851991452768`12.420319287159884, \ -4.73282767729390658976621877663379529011`12.413270226846409}, \ {-16.19843070253945098550579135288314672585`12.388473670567306, \ -5.13163898550832891453111688590796870884`12.381997431594007}, \ {-16.86633951670972288039471395655149173986`12.404954098342367, \ -5.80240199987962536791550503225958270863`12.398866130242835}, \ {-16.77689069495411182728224141955185035974`12.578732116047837, \ -6.23614513034919564437454337982825308836`12.573007556367687}, \ {-14.80252382100320164002240843623068768813`12.49306295102896, \ -5.91965063472591408534914272282390365534`12.488812443240525}, \ {-14.65491606802016362035886610245954042657`12.456470486972371, \ -6.28205120393482118528393372244886820757`12.452557890915463}, \ {-16.27439643519692633905092335784059883439`12.529381926564788, \ -7.45422174384778890401767542542167474554`12.525170715136564}, \ {-16.03166288483113939002153570592253254019`12.282114576362448, \ -7.82457713053242232215325990861999568481`12.278346619165035}, \ {-15.07454640526273004957137326935401409952`12.252825552630862, \ -7.82120582518507338465305329137100298858`12.249653271707373}, \ {-14.87943765022499528618810769547733726319`12.198902570148054, \ -8.18955403242119335710499148532961082149`12.196022608740064}, \ {-15.58946981937808421009103602841725058551`12.22588046088745, \ -9.08581372709906075451609021343336530992`12.223126660409362}, \ {-15.36317228865239776297461585717701385758`12.357014609112145, \ -9.4665090917491059732476437848304709201`12.354517626164647}, \ {-13.73996393097009503020043884955757919607`12.29665858898376, \ -8.93882704950339206711715046076941122524`12.294754652050147}, \ {-13.51678352511946764063949756018924961808`12.281339797978655, \ -9.27355520355267927648780384919252341398`12.279672783278025}, \ {-14.62600967521692407665565185975047118104`12.336460420994053, \ -10.57166886709404094385350508727999869072`12.33482948668552}, \ {-14.36121338370583901026703527728918026495`12.197408747710375, \ -10.92670272192400191303329057658731499646`12.196052396001102}, \ {-13.1715204508231318178564463702714497148`12.161023071193869, \ -10.54176645580352679561690308781703528033`12.160015058633508}, \ {-12.9005553820600193986289733345045683979`12.195944308249375, \ -10.85486121653440080979967474585300295858`12.195163654731974}, \ {-13.29951432537364693480477793879129676028`12.220805079653214, \ -11.75995210994669195309954755739061453851`12.220215169307831}, \ {-13.08033383578093545187455638451063579893`12.451140440968015, \ -12.15100846925880589912255305711810332331`12.450778113921825}, \ {-11.2546544628067141885803548753228414252`12.359309526416308, \ -10.98175891615689904504055205886873152193`12.35921249608267}, \ {-10.98175891615689904504055205886873152193`12.35921249608267, \ -11.2546544628067141885803548753228414252`12.359309526416308}, \ {-12.15100846925880589912255305711810332331`12.450778113921825, \ -13.08033383578093545187455638451063579893`12.451140440968015}, \ {-11.75995210994669195309954755739061453851`12.220215169307831, \ -13.29951432537364693480477793879129676028`12.220805079653214}, \ {-10.85486121653440080979967474585300295858`12.195163654731974, \ -12.9005553820600193986289733345045683979`12.195944308249375}, \ {-10.54176645580352679561690308781703528033`12.160015058633508, \ -13.1715204508231318178564463702714497148`12.161023071193869}, \ {-10.92670272192400191303329057658731499646`12.196052396001102, \ -14.36121338370583901026703527728918026495`12.197408747710375}, \ {-10.57166886709404094385350508727999869072`12.33482948668552, \ -14.62600967521692407665565185975047118104`12.336460420994053}, \ {-9.27355520355267927648780384919252341398`12.279672783278025, \ -13.51678352511946764063949756018924961808`12.281339797978655}, \ {-8.93882704950339206711715046076941122524`12.294754652050147, \ -13.73996393097009503020043884955757919607`12.29665858898376}, \ {-9.4665090917491059732476437848304709201`12.354517626164647, \ -15.36317228865239776297461585717701385758`12.357014609112145}, \ {-9.08581372709906075451609021343336530992`12.223126660409362, \ -15.58946981937808421009103602841725058551`12.22588046088745}, \ {-8.18955403242119335710499148532961082149`12.196022608740064, \ -14.87943765022499528618810769547733726319`12.198902570148054}, \ {-7.82120582518507338465305329137100298858`12.249653271707373, \ -15.07454640526273004957137326935401409952`12.252825552630862}, \ {-7.82457713053242232215325990861999568481`12.278346619165035, \ -16.03166288483113939002153570592253254019`12.282114576362448}, \ {-7.45422174384778890401767542542167474554`12.525170715136564, \ -16.27439643519692633905092335784059883439`12.529381926564788}, \ {-6.28205120393482118528393372244886820757`12.452557890915463, \ -14.65491606802016362035886610245954042657`12.456470486972371}, \ {-5.91965063472591408534914272282390365534`12.488812443240525, \ -14.80252382100320164002240843623068768813`12.49306295102896}, \ {-6.23614513034919564437454337982825308836`12.573007556367687, \ -16.77689069495411182728224141955185035974`12.578732116047837}, \ {-5.80240199987962536791550503225958270863`12.398866130242835, \ -16.86633951670972288039471395655149173986`12.404954098342367}, \ {-5.13163898550832891453111688590796870884`12.381997431594007, \ -16.19843070253945098550579135288314672585`12.388473670567306}, \ {-4.73282767729390658976621877663379529011`12.413270226846409, \ -16.32039786646297999355248712851991452768`12.420319287159884}, \ {-4.58743853522097220067597525896540520302`12.45136727422111, \ -17.40503264663657705311663298227568094025`12.46000235611703}, \ {-4.16142572435314229176423345359938562086`12.688624706216963, \ -17.52293990237707480842047458025435559075`12.698248087732606}, \ {-3.37234623886128944326115482292387787326`12.638018606413388, \ -15.92971359765875718878366413343512754734`12.647711235987842}, \ {-2.98179635397777571407074671727131017166`12.724275219282374, \ -16.01519969634362626065689788608629161345`12.735011257229134}, \ {-2.86338634623156299512264700209117639533`12.80146817857336, \ -17.79591112573248507455176046713722274677`12.816539964888452}, \ {-2.42505974872851272757153351585311094549`12.802700917173786, \ -17.85544245338604434451972861573455047732`12.819676047679714}, \ {-1.84609236164073767801421642041098441936`12.783432950664404, \ -16.64677301018509557615239237844633377422`12.803482938529699}, \ {-1.43441109943699839870141847779778349598`13.976665623639002, \ -16.65695381793228050808584203667069322301`14.000585243066286}, \ {-1.08187470605938232366812507645163314198`14.030008969967259, \ -17.60968320218134674574507427282472788876`14.068791427066426}, \ {-0.65552547220153738907967004084784565286`14.212249311922388, \ -17.79762844598512282344705390413118751706`14.22930702954548}, \ {-0.18943006612283838369614721865297608914`14.412947693365764, \ -15.43537558022916411709106513378718309858`14.499890161442933}, { 0.18943006612283838369614721865297216249`14.412947693365764, \ -15.4353755802291641170910651337871831468`14.499890161442933}, { 0.65552547220153738907967004084783206984`14.212249311922388, \ -17.79762844598512282344705390413118801741`14.22930702954548}, { 1.0818747060593823236681250764516107428`14.030008969967259, \ -17.60968320218134674574507427282472926485`14.068791427066426}, { 1.43441109943699839870141847779775383368`13.976665623639002, \ -16.65695381793228050808584203667069577736`14.000585243066286}, { 1.8460923616407376780142164204109429765`12.783432950664404, \ -16.64677301018509557615239237844633837012`12.803482938529699}, { 2.42505974872851272757153351585305026753`12.802700917173786, \ -17.85544245338604434451972861573455871842`12.819676047679714}, { 2.86338634623156299512264700209109974761`12.80146817857336, \ -17.79591112573248507455176046713723507949`12.816539964888452}, { 2.98179635397777571407074671727122663975`12.724275219282374, \ -16.01519969634362626065689788608630716584`12.735011257229134}, { 3.37234623886128944326115482292366245377`12.638018606413388, \ -15.92971359765875718878366413343517315203`12.647711235987842}, { 4.16142572435314229176423345359887344201`12.688624706216963, \ -17.52293990237707480842047458025447722532`12.698248087732606}, { 4.58743853522097220067597525896462310846`12.45136727422111, \ -17.4050326466365770531166329822758870767`12.46000235611703}, { 4.73282767729390658976621877663280560668`12.413270226846409, \ -16.32039786646297999355248712852020153052`12.420319287159884}, { 5.13163898550832891453111688590699790252`12.381997431594007, \ -16.19843070253945098550579135288345427585`12.388473670567306}, { 5.80240199987962536791550503225886068331`12.398866130242835, \ -16.86633951670972288039471395655174013295`12.404954098342367}, { 6.23614513034919564437454337982782217061`12.573007556367687, \ -16.77689069495411182728224141955201053637`12.578732116047837}, { 5.91965063472591408534914272282377692012`12.488812443240525, \ -14.8025238210032016400224084362307383706`12.49306295102896}, { 6.28205120393482118528393372244924436408`12.452557890915463, \ -14.65491606802016362035886610245937918138`12.456470486972371}, { 7.45422174384778890401767542542292791961`12.525170715136564, \ -16.27439643519692633905092335784002483848`12.529381926564788}, { 7.82457713053242232215325990862205315626`12.278346619165035, \ -16.03166288483113939002153570592152834962`12.282114576362448}, { 7.82120582518507338465305329137371148024`12.249653271707373, \ -15.07454640526273004957137326935260883858`12.252825552630862}, { 8.18955403242119335710499148533228722865`12.196022608740064, \ -14.8794376502249952861881076954758641847`12.198902570148054}, { 9.08581372709906075451609021343537537001`12.223126660409362, \ -15.58946981937808421009103602841607908764`12.22588046088745}, { 9.46650909174910597324764378483166926613`12.354517626164647, \ -15.36317228865239776297461585717627545848`12.357014609112145}, { 8.93882704950339206711715046076978310259`12.294754652050145, \ -13.73996393097009503020043884955733726328`12.296658588983759}, { 9.27355520355267927648780384913902504166`12.279672783278025, \ -13.51678352511946764063949756022595362448`12.281339797978655}, { 10.57166886709404094385350508710628615371`12.334829486685523, \ -14.62600967521692407665565185987603047295`12.336460420994054}, { 10.92670272192400191303329057630302043204`12.196052396001102, \ -14.36121338370583901026703527750548526003`12.197408747710375}, { 10.54176645580352679561690308745198609765`12.160015058633508, \ -13.17152045082313181785644637056361516709`12.161023071193869}, { 10.85486121653440080979967474549546100688`12.195163654731974, \ -12.9005553820600193986289733348054134506`12.195944308249375}, { 11.75995210994669195309954755712732940048`12.220215169307831, \ -13.29951432537364693480477793902410380415`12.220805079653214}, { 12.15100846925880589912255305696273565742`12.450778113921825, \ -13.08033383578093545187455638465496497641`12.451140440968015}, { 10.98175891615689904504055205882417074812`12.35921249608267, \ -11.25465446280671418858035487536632171829`12.359309526416308}, { 11.25465446280671418858035487655335785474`12.359309526416308, \ -10.98175891615689904504055205760763688938`12.35921249608267}, { 13.08033383578093545187455638859523162845`12.451140440968015, \ -12.15100846925880589912255305272111214603`12.450778113921825}, { 13.2995143253736469348047779453798653094`12.220805079653214, \ -11.75995210994669195309954754993949900821`12.220215169307831}, { 12.90055538206001939862897334301865035726`12.195944308249375, \ -10.85486121653440080979967473573436729353`12.195163654731974}, { 13.17152045082313181785644637853998449444`12.161023071193869, \ -10.54176645580352679561690307748582794384`12.160015058633508}, { 14.3612133837058390102670352834110125699`12.197408747710375, \ -10.92670272192400191303329056854125185488`12.196052396001102}, { 14.62600967521692407665565186330432177678`12.336460420994054, \ -10.57166886709404094385350508236321082585`12.334829486685523}, { 13.51678352511946764063949756122854962855`12.281339797978655, \ -9.27355520355267927648780384767767900414`12.279672783278025}, { 13.73996393097009503020043884974954717451`12.29665858898376, \ -8.93882704950339206711715046047433525113`12.294754652050147}, { 15.36317228865239776297461585778647293049`12.357014609112145, \ -9.46650909174910597324764378384138142072`12.354517626164647}, { 15.58946981937808421009103602939202534944`12.225880460887446, \ -9.0858137270990607545160902117608434841`12.223126660409358}, { 14.87943765022499528618810769670732770731`12.198902570148054, \ -8.18955403242119335710499148309486567549`12.196022608740064}, { 15.07454640526273004957137327052865944525`12.252825552630867, \ -7.82120582518507338465305328910699841312`12.249653271707379}, { 16.03166288483113939002153570676192659208`12.282114576362448, \ -7.82457713053242232215325990690017335525`12.278346619165035}, { 16.27439643519692633905092335832039698491`12.529381926564788, \ -7.45422174384778890401767542437415756941`12.525170715136564}, { 14.65491606802016362035886610259432384877`12.456470486972371, \ -6.28205120393482118528393372213444228583`12.452557890915463}, { 14.80252382100320164002240843623062057838`12.49306295102896, \ -5.91965063472591408534914272282407146821`12.488812443240525}, { 16.77689069495411182728224141955163826653`12.578732116047838, \ -6.23614513034919564437454337982882367554`12.57300755636769}, { 16.86633951670972288039471395655116283745`12.404954098342367, \ -5.80240199987962536791550503226053875755`12.398866130242835}, { 16.19843070253945098550579135288273949241`12.388473670567306, \ -5.1316389855083289145311168859092541739`12.381997431594007}, { 16.3203978664629799935524871285195389429`12.420319287159884, \ -4.73282767729390658976621877663509043417`12.413270226846409}, { 17.40503264663657705311663298227542090662`12.46000235611703, \ -4.58743853522097220067597525896639178718`12.45136727422111}, { 17.52293990237707480842047458025421405946`12.698248087732606, \ -4.16142572435314229176423345359998158138`12.688624706216963}, { 15.92971359765875718878366413343508931588`12.647711235987842, \ -3.37234623886128944326115482292405846472`12.638018606413388}, { 16.01519969634362626065689788608629161345`12.735011257229134, \ -2.98179635397777571407074671727131017166`12.724275219282374}, { 17.79591112573248507455176046713722274677`12.816539964888452, \ -2.86338634623156299512264700209117639533`12.80146817857336}, { 17.85544245338604434451972861573455047732`12.819676047679714, \ -2.42505974872851272757153351585311094549`12.802700917173786}, { 16.64677301018509557615239237844633377422`12.803482938529699, \ -1.84609236164073767801421642041098441936`12.783432950664404}, { 16.65695381793228050808584203667069322301`14.000585243066286, \ -1.43441109943699839870141847779778349598`13.976665623639002}, { 17.60968320218134674574507427282472788876`14.068791427066426, \ -1.08187470605938232366812507645163314198`14.030008969967259}, { 17.79762844598512282344705390413118751706`14.22930702954548, \ -0.65552547220153738907967004084784565286`14.212249311922388}, { 15.43537558022916411709106513378718309858`14.499890161442933, \ -0.18943006612283838369614721865297608914`14.412947693365764}, { 15.4353755802291641170910651337871831468`14.499890161442933, 0.18943006612283838369614721865297216249`14.412947693365764}, { 17.79762844598512282344705390413118801741`14.22930702954548, 0.65552547220153738907967004084783206984`14.212249311922388}, { 17.60968320218134674574507427282472926485`14.068791427066426, 1.0818747060593823236681250764516107428`14.030008969967259}, { 16.65695381793228050808584203667069577736`14.000585243066286, 1.43441109943699839870141847779775383368`13.976665623639002}, { 16.64677301018509557615239237844633837012`12.803482938529699, 1.8460923616407376780142164204109429765`12.783432950664404}, { 17.85544245338604434451972861573455871842`12.819676047679714, 2.42505974872851272757153351585305026753`12.802700917173786}, { 17.79591112573248507455176046713723507949`12.816539964888452, 2.86338634623156299512264700209109974761`12.80146817857336}, { 16.01519969634362626065689788608630716584`12.735011257229134, 2.98179635397777571407074671727122663975`12.724275219282374}, { 15.92971359765875718878366413343513492052`12.647711235987842, 3.37234623886128944326115482292384304523`12.638018606413388}, { 17.52293990237707480842047458025433569393`12.698248087732606, 4.16142572435314229176423345359946940258`12.688624706216963}, { 17.40503264663657705311663298227562704302`12.46000235611703, 4.58743853522097220067597525896560969257`12.45136727422111}, { 16.32039786646297999355248712851982594579`12.420319287159884, 4.73282767729390658976621877663410075069`12.413270226846409}, { 16.19843070253945098550579135288304704241`12.388473670567306, 5.13163898550832891453111688590828336757`12.381997431594007}, { 16.86633951670972288039471395655141123048`12.404954098342367, 5.80240199987962536791550503225981673222`12.398866130242835}, { 16.77689069495411182728224141955179844316`12.578732116047838, 6.23614513034919564437454337982839275779`12.57300755636769}, { 14.80252382100320164002240843623067126085`12.49306295102896, 5.9196506347259140853491427228239447329`12.488812443240525}, { 14.65491606802016362035886610259416260363`12.456470486972371, 6.28205120393482118528393372213481844238`12.452557890915463}, { 16.27439643519692633905092335831982298901`12.529381926564788, 7.45422174384778890401767542437541074338`12.525170715136564}, { 16.03166288483113939002153570676092240157`12.282114576362448, 7.82457713053242232215325990690223082675`12.278346619165035}, { 15.0745464052627300495713732705272541843`12.252825552630867, 7.82120582518507338465305328910970690488`12.249653271707379}, { 14.87943765022499528618810769670585462872`12.198902570148054, 8.18955403242119335710499148309754208254`12.196022608740064}, { 15.58946981937808421009103602939085385158`12.225880460887446, 9.08581372709906075451609021176285354403`12.223126660409358}, { 15.36317228865239776297461585778573453139`12.357014609112145, 9.46650909174910597324764378384257976653`12.354517626164647}, { 13.73996393097009503020043884974930524181`12.29665858898376, 8.93882704950339206711715046047470712833`12.294754652050147}, { 13.5167835251194676406394975612652536351`12.281339797978655, 9.27355520355267927648780384762418063162`12.279672783278025}, { 14.62600967521692407665565186342988106901`12.336460420994054, 10.57166886709404094385350508218949828852`12.334829486685523}, { 14.3612133837058390102670352836273175652`12.197408747710375, 10.92670272192400191303329056825695729014`12.196052396001102}, { 13.17152045082313181785644637883214994677`12.161023071193869, 10.54176645580352679561690307712077876101`12.160015058633508}, { 12.90055538206001939862897334331949541015`12.195944308249375, 10.85486121653440080979967473537682534168`12.195163654731974}, { 13.29951432537364693480477794561267235342`12.220805079653214, 11.75995210994669195309954754967621386992`12.220215169307831}, { 13.08033383578093545187455638873956080619`12.451140440968015, 12.15100846925880589912255305256574447983`12.450778113921825}, { 11.25465446280671418858035487659683814801`12.359309526416308, 10.98175891615689904504055205756307611552`12.35921249608267}, { 10.98175891615689904504055205756307611557`12.35921249608267, 11.25465446280671418858035487659683814778`12.359309526416308}, { 12.15100846925880589912255305256574448009`12.450778113921825, 13.08033383578093545187455638873956080598`12.451140440968015}, { 11.75995210994669195309954754967621387018`12.220215169307831, 13.29951432537364693480477794561267235327`12.220805079653214}, { 10.85486121653440080979967473537682534182`12.195163654731974, 12.90055538206001939862897334331949541`12.195944308249375}, { 10.54176645580352679561690307712077876111`12.160015058633508, 13.17152045082313181785644637883214994667`12.161023071193869}, { 10.9267027219240019130332905682569572903`12.196052396001102, 14.36121338370583901026703528362731756504`12.197408747710375}, { 10.57166886709404094385350508218949828868`12.334829486685523, 14.62600967521692407665565186342988106885`12.336460420994054}, { 9.27355520355267927648780384762418063181`12.279672783278025, 13.51678352511946764063949756126525363491`12.281339797978655}, { 8.93882704950339206711715046047470712838`12.294754652050145, 13.73996393097009503020043884974930524171`12.296658588983759}, { 9.46650909174910597324764378384257976653`12.354517626164647, 15.36317228865239776297461585778573453139`12.357014609112145}, { 9.08581372709906075451609021176285354403`12.223126660409358, 15.58946981937808421009103602939085385158`12.225880460887446}, { 8.18955403242119335710499148309754208254`12.196022608740064, 14.87943765022499528618810769670585462872`12.198902570148054}, { 7.82120582518507338465305328910970690488`12.249653271707379, 15.0745464052627300495713732705272541843`12.252825552630867}, { 7.82457713053242232215325990690223082675`12.278346619165035, 16.03166288483113939002153570676092240157`12.282114576362448}, { 7.45422174384778890401767542437541074338`12.525170715136564, 16.27439643519692633905092335831982298901`12.529381926564788}, { 6.28205120393482118528393372213481844238`12.452557890915463, 14.65491606802016362035886610259416260363`12.456470486972371}, { 5.9196506347259140853491427228239447329`12.488812443240525, 14.80252382100320164002240843623067126085`12.49306295102896}, { 6.23614513034919564437454337982839275779`12.57300755636769, 16.77689069495411182728224141955179844316`12.578732116047838}, { 5.80240199987962536791550503225981673222`12.398866130242835, 16.86633951670972288039471395655141123048`12.404954098342367}, { 5.13163898550832891453111688590828336757`12.381997431594007, 16.19843070253945098550579135288304704241`12.388473670567306}, { 4.73282767729390658976621877663410075069`12.413270226846409, 16.32039786646297999355248712851982594579`12.420319287159884}, { 4.58743853522097220067597525896560969257`12.45136727422111, 17.40503264663657705311663298227562704302`12.46000235611703}, { 4.16142572435314229176423345359946940258`12.688624706216963, 17.52293990237707480842047458025433569393`12.698248087732606}, { 3.37234623886128944326115482292384304523`12.638018606413388, 15.92971359765875718878366413343513492052`12.647711235987842}, { 2.98179635397777571407074671727122663975`12.724275219282374, 16.01519969634362626065689788608630716584`12.735011257229134}, { 2.86338634623156299512264700209109974761`12.80146817857336, 17.79591112573248507455176046713723507949`12.816539964888452}, { 2.42505974872851272757153351585305026753`12.802700917173786, 17.85544245338604434451972861573455871842`12.819676047679714}, { 1.8460923616407376780142164204109429765`12.783432950664404, 16.64677301018509557615239237844633837012`12.803482938529699}, { 1.43441109943699839870141847779775383368`13.976665623639002, 16.65695381793228050808584203667069577736`14.000585243066286}, { 1.0818747060593823236681250764516107428`14.030008969967259, 17.60968320218134674574507427282472926485`14.068791427066426}, { 0.65552547220153738907967004084783206984`14.212249311922388, 17.79762844598512282344705390413118801741`14.22930702954548}, { 0.18943006612283838369614721865297216249`14.412947693365764, 15.4353755802291641170910651337871831468`14.499890161442933}, \ {-0.18943006612283838369614721865297608914`14.412947693365764, 15.43537558022916411709106513378718309858`14.499890161442933}, \ {-0.65552547220153738907967004084784565286`14.212249311922388, 17.79762844598512282344705390413118751706`14.22930702954548}, \ {-1.08187470605938232366812507645163314198`14.030008969967259, 17.60968320218134674574507427282472788876`14.068791427066426}, \ {-1.43441109943699839870141847779778349598`13.976665623639002, 16.65695381793228050808584203667069322301`14.000585243066286}, \ {-1.84609236164073767801421642041098441936`12.783432950664404, 16.64677301018509557615239237844633377422`12.803482938529699}, \ {-2.42505974872851272757153351585311094549`12.802700917173786, 17.85544245338604434451972861573455047732`12.819676047679714}, \ {-2.86338634623156299512264700209117639533`12.80146817857336, 17.79591112573248507455176046713722274677`12.816539964888452}, \ {-2.98179635397777571407074671727131017166`12.724275219282374, 16.01519969634362626065689788608629161345`12.735011257229134}, \ {-3.37234623886128944326115482292405846472`12.638018606413388, 15.92971359765875718878366413343508931588`12.647711235987842}, \ {-4.16142572435314229176423345359998158138`12.688624706216963, 17.52293990237707480842047458025421405946`12.698248087732606}, \ {-4.58743853522097220067597525896639178718`12.45136727422111, 17.40503264663657705311663298227542090662`12.46000235611703}, \ {-4.73282767729390658976621877663509043417`12.413270226846409, 16.3203978664629799935524871285195389429`12.420319287159884}, \ {-5.1316389855083289145311168859092541739`12.381997431594007, 16.19843070253945098550579135288273949241`12.388473670567306}, \ {-5.80240199987962536791550503226053875755`12.398866130242835, 16.86633951670972288039471395655116283745`12.404954098342367}, \ {-6.23614513034919564437454337982882367554`12.57300755636769, 16.77689069495411182728224141955163826653`12.578732116047838}, \ {-5.91965063472591408534914272282407146821`12.488812443240525, 14.80252382100320164002240843623062057838`12.49306295102896}, \ {-6.28205120393482118528393372213444228583`12.452557890915463, 14.65491606802016362035886610259432384877`12.456470486972371}, \ {-7.45422174384778890401767542437415756941`12.525170715136564, 16.27439643519692633905092335832039698491`12.529381926564788}, \ {-7.82457713053242232215325990690017335525`12.278346619165035, 16.03166288483113939002153570676192659208`12.282114576362448}, \ {-7.82120582518507338465305328910699841312`12.249653271707379, 15.07454640526273004957137327052865944525`12.252825552630867}, \ {-8.18955403242119335710499148309486567549`12.196022608740064, 14.87943765022499528618810769670732770731`12.198902570148054}, \ {-9.0858137270990607545160902117608434841`12.223126660409358, 15.58946981937808421009103602939202534944`12.225880460887446}, \ {-9.46650909174910597324764378384138142072`12.354517626164647, 15.36317228865239776297461585778647293049`12.357014609112145}, \ {-8.93882704950339206711715046047433525113`12.294754652050147, 13.73996393097009503020043884974954717451`12.29665858898376}, \ {-9.27355520355267927648780384767767900414`12.279672783278025, 13.51678352511946764063949756122854962855`12.281339797978655}, \ {-10.57166886709404094385350508236321082585`12.334829486685523, 14.62600967521692407665565186330432177678`12.336460420994054}, \ {-10.92670272192400191303329056854125185488`12.196052396001102, 14.3612133837058390102670352834110125699`12.197408747710375}, \ {-10.54176645580352679561690307748582794384`12.160015058633508, 13.17152045082313181785644637853998449444`12.161023071193869}, \ {-10.85486121653440080979967473573436729353`12.195163654731974, 12.90055538206001939862897334301865035726`12.195944308249375}, \ {-11.75995210994669195309954754993949900821`12.220215169307831, 13.2995143253736469348047779453798653094`12.220805079653214}, \ {-12.15100846925880589912255305272111214603`12.450778113921825, 13.08033383578093545187455638859523162845`12.451140440968015}, \ {-10.98175891615689904504055205760763688938`12.35921249608267, 11.25465446280671418858035487655335785474`12.359309526416308}, \ {-11.25465446280671418858035487536632171843`12.359309526416308, 10.98175891615689904504055205882417074803`12.35921249608267}, \ {-13.08033383578093545187455638465496497667`12.451140440968015, 12.15100846925880589912255305696273565721`12.450778113921825}, \ {-13.29951432537364693480477793902410380436`12.220805079653214, 11.75995210994669195309954755712732940027`12.220215169307831}, \ {-12.90055538206001939862897333480541345075`12.195944308249375, 10.85486121653440080979967474549546100673`12.195163654731974}, \ {-13.17152045082313181785644637056361516719`12.161023071193869, 10.54176645580352679561690308745198609741`12.160015058633508}, \ {-14.36121338370583901026703527750548526024`12.197408747710375, 10.92670272192400191303329057630302043183`12.196052396001102}, \ {-14.62600967521692407665565185987603047321`12.336460420994053, 10.57166886709404094385350508710628615355`12.33482948668552}, \ {-13.51678352511946764063949756022595362448`12.281339797978655, 9.27355520355267927648780384913902504156`12.279672783278025}, \ {-13.73996393097009503020043884955733726337`12.29665858898376, 8.9388270495033920671171504607697831025`12.294754652050147}, \ {-15.36317228865239776297461585717627545848`12.357014609112145, 9.46650909174910597324764378483166926613`12.354517626164647}, \ {-15.58946981937808421009103602841607908764`12.22588046088745, 9.08581372709906075451609021343537537001`12.223126660409362}, \ {-14.8794376502249952861881076954758641847`12.198902570148054, 8.18955403242119335710499148533228722865`12.196022608740064}, \ {-15.07454640526273004957137326935260883858`12.252825552630862, 7.82120582518507338465305329137371148024`12.249653271707373}, \ {-16.03166288483113939002153570592152834962`12.282114576362448, 7.82457713053242232215325990862205315626`12.278346619165035}, \ {-16.27439643519692633905092335784002483848`12.529381926564788, 7.45422174384778890401767542542292791961`12.525170715136564}, \ {-14.65491606802016362035886610245937918138`12.456470486972371, 6.28205120393482118528393372244924436408`12.452557890915463}, \ {-14.8025238210032016400224084362307383706`12.49306295102896, 5.91965063472591408534914272282377692012`12.488812443240525}, \ {-16.77689069495411182728224141955201053637`12.578732116047837, 6.23614513034919564437454337982782217061`12.573007556367687}, \ {-16.86633951670972288039471395655174013295`12.404954098342367, 5.80240199987962536791550503225886068331`12.398866130242835}, \ {-16.19843070253945098550579135288345427585`12.388473670567306, 5.13163898550832891453111688590699790252`12.381997431594007}, \ {-16.32039786646297999355248712852020153052`12.420319287159884, 4.73282767729390658976621877663280560668`12.413270226846409}, \ {-17.4050326466365770531166329822758870767`12.46000235611703, 4.58743853522097220067597525896462310846`12.45136727422111}, \ {-17.52293990237707480842047458025447722532`12.698248087732606, 4.16142572435314229176423345359887344201`12.688624706216963}, \ {-15.92971359765875718878366413343517315203`12.647711235987842, 3.37234623886128944326115482292366245377`12.638018606413388}, \ {-16.01519969634362626065689788608630716584`12.735011257229134, 2.98179635397777571407074671727122663975`12.724275219282374}, \ {-17.79591112573248507455176046713723507949`12.816539964888452, 2.86338634623156299512264700209109974761`12.80146817857336}, \ {-17.85544245338604434451972861573455871842`12.819676047679714, 2.42505974872851272757153351585305026753`12.802700917173786}, \ {-16.64677301018509557615239237844633837012`12.803482938529699, 1.8460923616407376780142164204109429765`12.783432950664404}, \ {-16.65695381793228050808584203667069577736`14.000585243066286, 1.43441109943699839870141847779775383368`13.976665623639002}, \ {-17.60968320218134674574507427282472926485`14.068791427066426, 1.0818747060593823236681250764516107428`14.030008969967259}, \ {-17.79762844598512282344705390413118801741`14.22930702954548, 0.65552547220153738907967004084783206984`14.212249311922388}, \ {-15.4353755802291641170910651337871831468`14.499890161442933, 0.18943006612283838369614721865297216249`14.412947693365764}, \ {-15.43537558022916411709106513378718309858`14.499890161442933, \ -0.18943006612283838369614721865297608914`14.412947693365764}}; triangles = CompressedData[" 1:eJxVmGW4VWUUhGcwELtbEbu7W1CxA7sRu8DuQLEwMcHGFgzsDuzubuzubu+4 hmc+f5znvFzu3fu7+6w18z63W59+vfp2AvA3gTE63jveoH+P5jHx/6+P0/x/ Z7/re8b2u75vLL/reydufm4is35uwuYaE5h1jfGb641n1vXGba7dxaxrz9Tc p2tznxl9L/EMZt1z+ub+0zX3n9ZnEE9j1lmmbs41VXOuKX028RRmnXHy5ryT Need1GcWT2LWe7fmazM33zuLf1Y8q1nXm6259uzNPefwGcRzmnWuuZozzt2c fR7/LuJ5zfr95mt+1/mbZ7CAn4l4QbOe00LNM1u4eZaL+NmKFzXreS/WPPvF m89kCX9G4iXN+tyWaj7DpZvPdhl/1uJlzfr8l0NmYXlkRlbwMxev2Fx7peba 3X19cQ+z7rNyc89Vmnuu6vuKe5p1/9Was6zenGUNn0e8plnnWqs549rNGdfx mcXrmjUv6yGzsz4yO71Q8yPewKw52hCZqY2QmdoYNVfiTcyar02RWdsMmbXN UfMm3sKsudsSmcGtkBncGjWH4m3MmsfeyGxui8xmH9R8ircza063R2Z2B2Rm d0TNrXgns+Z3Z2SWd0FmeVfUPIt3M2uud0dmfA9kxvui5lzcz6x53xOZ/b2Q 2d8bNf/ifczag32RndgP2Yn9UXshPsCs/TgQ2ZWDkF05GLUv4kPM2ptDkR06 DNmhw1F7JD7CrJnv37wfiezBUahdEA8wayeORvbjGGQ/jkXtiPg4s3bleGRv BiJ7cwJqd8QnmrVDJyH7dDKyT6egdkp8qlm7NQjZs9OQPTsdtWviM8zauTOR /TsL2b+zUTsoHmzWLg5B9vIcZC/PRe2m+DyzdvR8ZF8vQPb1QtTOii8ya3eH Int8MbLHl6B2WXypWTt9GbLflyP7fQVqx8VXmrXrVyF7PwzZ++Go3RdfbVYG XIPkwbVIHlyHygTxCLOy4XokJ25AcuJGVFaIbzIrM25G8uMWJD9uRWWI+Daz suR2JFfuQHLlTlS2iO8yK2PuRvLmHiRv7kVljvg+c++O10gkh+5HcugBVBaJ HzQrkx5C8ulhJJ8eQWWU+FGzsuoxJLceR3LrCVR2iZ80K8OeQvLsaSTPnkFl mvhZs7LtOSTnnkdy7gVU1olfNCvzXkLy72Uk/15BZaD4VbOy8DUkF19HcvEN VDaK3zQrI99C8vJtJC/fQWWm+F2zsnMUkqPvITn6PipLxR+YlakfIvn6EZKv H6MyVvyJWVn7KZK7nyG5+zkqe8VfmJXBXyJ5/BWSx1+jMln8jVnZ/C2S098h Of09KqvFP5iV2T8i+f0Tkt8/ozJc/ItZWf4rkuu/Ibn+OyrbxX+YlfF/Inn/ F5L3f6MyX/yPuX/HS0E0+p1MD3RidYF4DLM6YUymH8Zi+mFsVkeIO5vVFeMw vdGF6Y1xWd0hHs+sDhmf6ZMJmD6ZkNUp/3WLWd0yMdMzkzA9Mymra8STmdU5 kzP9MwXTP1OyOkg8lVldNDXTS9MwvTQtq5vE05nVUdMzfTUD01czsjpL3NWs 7pqJ6bFuTI/NzOoy8SxmddqsTL/NxvTb7KyOE89hVtfNyfTeXEzvzc3qPvE8 ZnXgvEwfzsf04fysThQvYFY3Lsj05EJMTy7M6krxImZ15qJMfy7G9OfirA4V L2FWly7J9OpSTK8uzepW8TJmdeyyTN8ux/Tt8qzOFa9gHtrxWpHp4ZWYHu7O 6mJxD7M6eWWmn1dh+nlVVkeLe5rV1asxvb0609trsLpbvKZZHb4W0+drM32+ DqvTxeua1e3rMT2/PtPzvVhdL97ArM7fkOn/jZj+35jlAOJNzHKBTRkv2Izx gs1ZbiDewixH2JLxha0YX9ia5Qzibcxyh96MR2zLeEQflkuItzPLKbZn/GIH xi92ZDmGeCezXGNnxjt2YbxjV5Z7iHczy0F2Z3xkD8ZH+rKcRNzPLDfZk/GU vRhP2ZvlKuJ9zHKWfRl/2Y/xl/1ZDiM+wCyXOZDxmoMYrzmY5TbiQ8xynEMZ 3zmM8Z3DWc4jPsI8suPVn/GgIxkPOorlQuIBZjnR0YwfHcP40bEsRxIfZ5Yr Hc9400DGm05guZP4RLMc6iTGp05mfOoUllOJTzXLrQYxnnUa41mns1xLfIZZ znUm419nMf51NsvBxIPNcrEhjJedw3jZuSw3E59nlqOdz/jaBYyvXchyNvFF ZrnbUMbjLmY87hKWy4kvNcvpLmP87nLG765gOZ74SrNc7yrG+4Yx3jec5X7i q81ywGsYH7yW8cHrWE4oHmGWG17PeOINjCfeyHJF8U1mOePNjD/ewvjjrSyH FN9mlkveznjlHYxX3slyS/FdZjnm3Yxv3sP45r0s5xTfZx7V8RrJeOj9jIc+ wHJR8YNmOelDjJ8+zPjpIyxHFT9qlqs+xnjr44y3PsFyV/GTZjnsU4zPPs34 7DMspxU/a5bbPsd47vOM577Acl3xi2Y570uM/77M+O8rLAcWv2qWC7/GePHr jBe/wXJj8ZtmOfJbjC+/zfjyOyxnFr9rljuPYjz6Pcaj32e5tPgDs5z6Q8av P2L8+mOWY4s/Mcu1P2W8+zPGuz9nubf4C7Mc/EvGx79ifPxrlpOLvzHLzb9l PP07xtO/Z7m6+AeznP1Hxt9/Yvz9Z5bDi38xy+V/Zbz+N8brf2e5vfgPsxz/ T8b3/2J8X3/T72T+xzz6D/n/AhvQWCk= "]; Table[ ResourceFunction["WolframModelPlot"][ Union[Sort /@ Catenate[Partition[#, 2, 1, 1] & /@ Take[triangles, 2^n - 2]]], VertexCoordinates -> Thread[Range[512] -> pts], "ArrowheadLength" -> 0, "MaxImageSize" -> 100], {n, 2, 7}]

If we tried to render this with every triangle roughly the same size, then even in 3D the best we could do would be to have something that crinkles up more and more at the edge, like an idealized lettuce leaf:

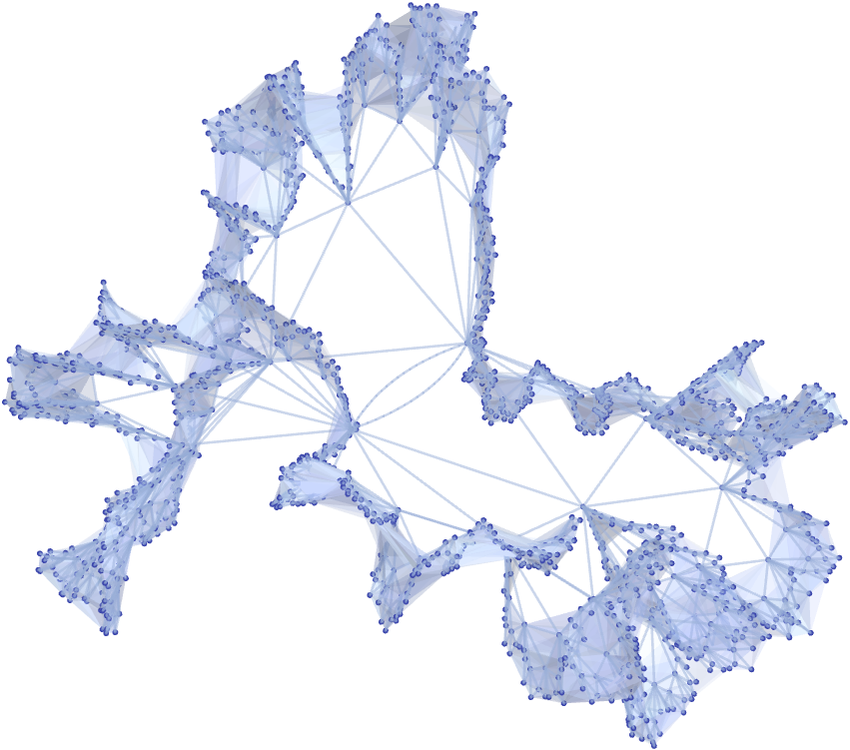
CloudGet["https://wolfr.am/LDlGWNOC"]; ResourceFunction["GraphReconstructedSurface"][ List @@@ EdgeList[hgraph[10]], 2, EdgeStyle -> Directive[AbsoluteThickness[1.3], Hue[0.61, 0.3, 0.85]], VertexSize -> 2, VertexStyle -> Directive[Hue[0.65, 0.64, 0.68], Specularity[Hue[0.71, 0.6, 0.64], 10]]]

But just as we can think of the grids we discussed before as being regularly laid out in ordinary 2D or 3D space, so now we can think of the object we have here as being regularly laid out in a hyperbolic space [19][20] of constant negative curvature.

In particular, the object corresponds to an infinite-order triangular tiling of the hyperbolic plane (with Schläfli symbol {3,∞}). There are a variety of ways to visualize the hyperbolic plane. One example is the Poincaré disk model in which hyperbolic-space straight lines are rendered as arcs of circles orthogonal to the boundary:

CloudGet["https://wolfr.am/LDlGWNOC"]; Table[Graphics[{{LightGray, Circle[]}, Style[{Line[{{0, -1}, {0, 1}}], Table[ PLine[#[[1]], #[[2]]] & /@ N[Partition[Table[2 k Pi/(2^n), {k, 0, 2^n - 1}], 2, 1, 1]], {n, 1, step + 1}]}, ResourceFunction["WolframPhysicsProjectStyleData"][ "SpatialGraph"]["EdgeLineStyle"]]}, ImageSize -> 130, PlotRange -> {{-1, 1}, {-1, 1}}], {step, 5}]

(The particular graph here happens to be the Farey graph [21].)

  • Download Notebook
  • Open in Wolfram Cloud
  • Discuss This Page